Question Number 65102 by da last updated on 25/Jul/19
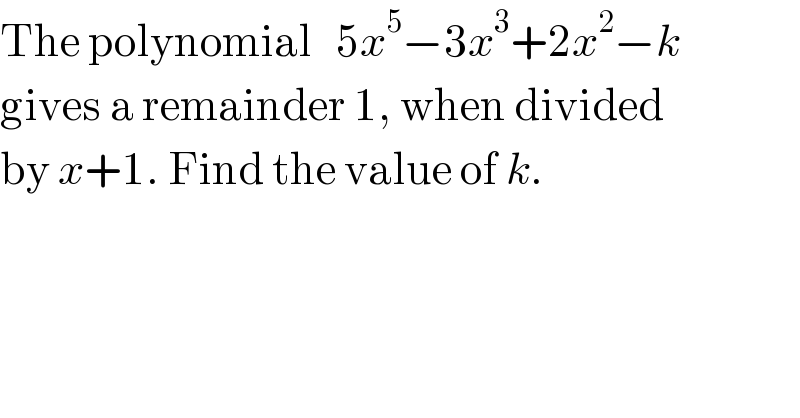
$$\mathrm{The}\:\mathrm{polynomial}\:\:\:\mathrm{5}{x}^{\mathrm{5}} −\mathrm{3}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −{k}\: \\ $$$$\mathrm{gives}\:\mathrm{a}\:\mathrm{remainder}\:\mathrm{1},\:\mathrm{when}\:\mathrm{divided} \\ $$$$\mathrm{by}\:{x}+\mathrm{1}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{k}. \\ $$
Commented by ~ À ® @ 237 ~ last updated on 25/Jul/19

$$\:{let}\:{p}\left({x}\right)=\mathrm{5}{x}^{\mathrm{5}} −\mathrm{3}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −{k}\:\:\:\:\:\:.\:{if}\:{the}\:{remainder}\:{is}\:\mathrm{1}\:{that}\:{means}\:{p}\left(−\mathrm{1}\right)=\mathrm{1}.\:{And}\:{easily}\:{we}\:{prove}\:{that} \\ $$$${p}\left(−\mathrm{1}\right)=\mathrm{1}\:\:\Rightarrow\:{k}=−\mathrm{1} \\ $$
Answered by Rio Michael last updated on 25/Jul/19
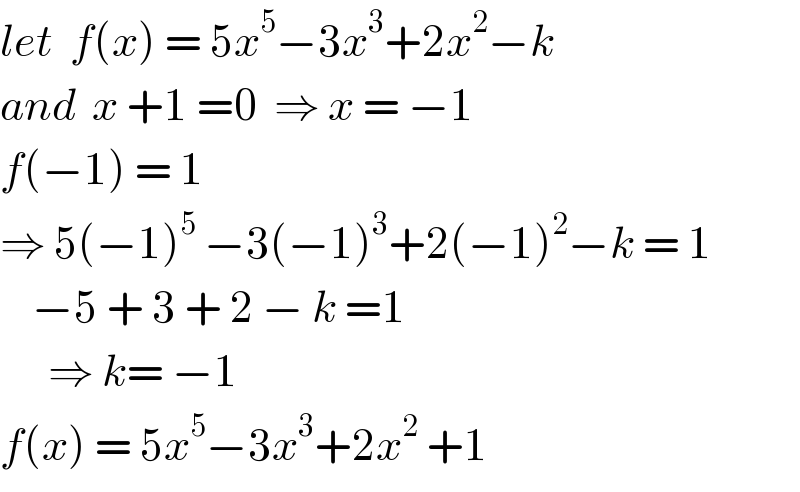
$${let}\:\:{f}\left({x}\right)\:=\:\mathrm{5}{x}^{\mathrm{5}} −\mathrm{3}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −{k} \\ $$$${and}\:\:{x}\:+\mathrm{1}\:=\mathrm{0}\:\:\Rightarrow\:{x}\:=\:−\mathrm{1} \\ $$$${f}\left(−\mathrm{1}\right)\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{5}\left(−\mathrm{1}\right)^{\mathrm{5}} \:−\mathrm{3}\left(−\mathrm{1}\right)^{\mathrm{3}} +\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{2}} −{k}\:=\:\mathrm{1} \\ $$$$\:\:\:\:−\mathrm{5}\:+\:\mathrm{3}\:+\:\mathrm{2}\:−\:{k}\:=\mathrm{1} \\ $$$$\:\:\:\:\:\:\Rightarrow\:{k}=\:−\mathrm{1} \\ $$$${f}\left({x}\right)\:=\:\mathrm{5}{x}^{\mathrm{5}} −\mathrm{3}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1} \\ $$
