Question Number 72046 by aliesam last updated on 23/Oct/19

Commented by mathmax by abdo last updated on 26/Oct/19
![let U_n =∫_0 ^1 nln(1+((x/n))^α )dx ⇒U_n =_((x/n)=t) ∫_0 ^(1/n) nln(1+t^α )ndt =n^2 ∫_0 ^(1/n) ln(1+t^α )dt but 0<t<(1/n) and n→+∞ ln(1+t^α )∼t^α ⇒ U_n ∼n^2 ∫_0 ^(1/n) t^α dt =n^2 [(1/(α+1))t^(α+1) ]_0 ^(1/n) =(n^2 /(α+1))((1/n))^(α+1) =(1/((α+1)n^(α+1−2) )) =(1/((α+1)n^(α−1) )) =(n^(1−α) /((α+1))) →+∞ because 1−α>0 another way U_n =∫_R nln(1+((x/n))^α ) χ_([0,1]) (x)dx=∫_(R ) f_n (x)dx we have f_n (x)∼n((x/n))^α =((nx^n )/n^n ) =(x^α /n^(α−1) ) =n^(1−α) x^α but 1−α>0 ⇒ f_n (x)→+∞ (n→+∞) ⇒lim_(n→+∞) U_n =+∞](https://www.tinkutara.com/question/Q72263.png)
$${let}\:{U}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} {nln}\left(\mathrm{1}+\left(\frac{{x}}{{n}}\right)^{\alpha} \right){dx}\:\Rightarrow{U}_{{n}} =_{\frac{{x}}{{n}}={t}} \:\:\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{{n}}} {nln}\left(\mathrm{1}+{t}^{\alpha} \right){ndt} \\ $$$$={n}^{\mathrm{2}} \int_{\mathrm{0}} ^{\frac{\mathrm{1}}{{n}}} \:{ln}\left(\mathrm{1}+{t}^{\alpha} \right){dt}\:\:\:{but}\:\:\mathrm{0}<{t}<\frac{\mathrm{1}}{{n}}\:{and}\:{n}\rightarrow+\infty\:\:{ln}\left(\mathrm{1}+{t}^{\alpha} \right)\sim{t}^{\alpha} \:\Rightarrow \\ $$$${U}_{{n}} \sim{n}^{\mathrm{2}} \int_{\mathrm{0}} ^{\frac{\mathrm{1}}{{n}}} {t}^{\alpha} {dt}\:={n}^{\mathrm{2}} \left[\frac{\mathrm{1}}{\alpha+\mathrm{1}}{t}^{\alpha+\mathrm{1}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{{n}}} =\frac{{n}^{\mathrm{2}} }{\alpha+\mathrm{1}}\left(\frac{\mathrm{1}}{{n}}\right)^{\alpha+\mathrm{1}} =\frac{\mathrm{1}}{\left(\alpha+\mathrm{1}\right){n}^{\alpha+\mathrm{1}−\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\left(\alpha+\mathrm{1}\right){n}^{\alpha−\mathrm{1}} }\:=\frac{{n}^{\mathrm{1}−\alpha} }{\left(\alpha+\mathrm{1}\right)}\:\rightarrow+\infty\:\:{because}\:\mathrm{1}−\alpha>\mathrm{0} \\ $$$${another}\:{way}\:{U}_{{n}} =\int_{{R}} \:{nln}\left(\mathrm{1}+\left(\frac{{x}}{{n}}\right)^{\alpha} \right)\:\chi_{\left[\mathrm{0},\mathrm{1}\right]} \left({x}\right){dx}=\int_{{R}\:} \:\:{f}_{{n}} \left({x}\right){dx} \\ $$$${we}\:{have}\:{f}_{{n}} \left({x}\right)\sim{n}\left(\frac{{x}}{{n}}\right)^{\alpha} \:=\frac{{nx}^{{n}} }{{n}^{{n}} }\:=\frac{{x}^{\alpha} }{{n}^{\alpha−\mathrm{1}} }\:={n}^{\mathrm{1}−\alpha} \:{x}^{\alpha} \:\:{but}\:\mathrm{1}−\alpha>\mathrm{0}\:\Rightarrow \\ $$$${f}_{{n}} \left({x}\right)\rightarrow+\infty\:\left({n}\rightarrow+\infty\right)\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:\:\:{U}_{{n}} =+\infty \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 26/Oct/19
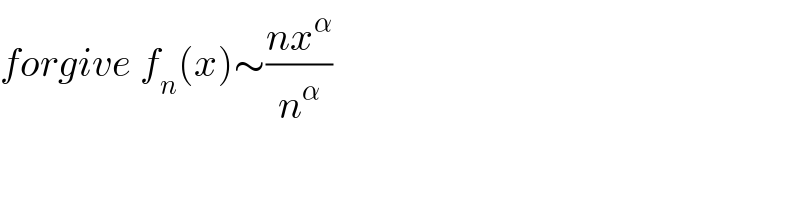
$${forgive}\:{f}_{{n}} \left({x}\right)\sim\frac{{nx}^{\alpha} }{{n}^{\alpha} } \\ $$
