Question Number 131602 by rs4089 last updated on 06/Feb/21
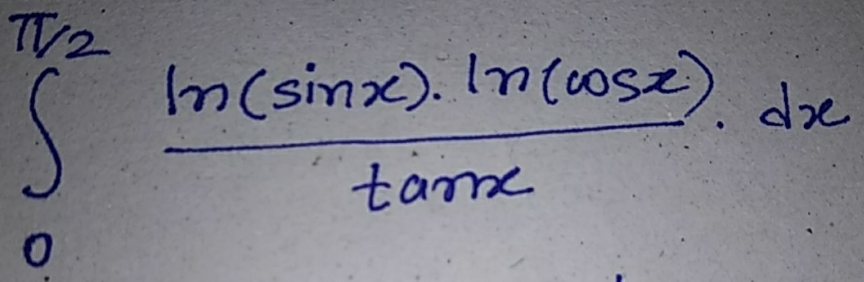
Answered by mnjuly1970 last updated on 06/Feb/21

$$\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{8}} \\ $$
Answered by mathmax by abdo last updated on 06/Feb/21
![Φ =∫_0 ^(π/2) ((ln(sinx).ln(cosx))/(tanx))dx let ϕ(a) =∫_0 ^(π/2) ((ln(asinx)ln(cosx))/(tanx))dx ⇒ ϕ^′ (a) =∫_0 ^(π/2) ((sinx)/(asinx)).((ln(cosx))/(tanx))dx =(1/a)∫_0 ^(π/2) ((ln(cosx))/(tanx))dx =(1/a)∫_0 ^(π/2) ((ln((√(1/(1+tan^2 x)))))/(tanx))dx =_(tanx=t) (1/a)∫_0 ^∞ ((ln((1/( (√(1+t^2 ))))))/t)×(dt/(1+t^2 )) =−(1/(2a))∫_0 ^∞ ((ln(1+t^2 ))/(t(1+t^2 )))dt and ∫_0 ^∞ ((ln(1+t^2 ))/(t(1+t^2 )))dt=∫_0 ^1 (...)dt +∫_1 ^∞ (..(√()dt)) ∫_1 ^∞ (...)dt =_(t=(1/u)) −∫_0 ^1 u((ln(1+(1/u^2 )))/((1+(1/u^2 ))))(−(du/u^2 )) =∫_0 ^1 u((ln(1+u^2 )−2lnu)/(u^2 +1))du =∫_0 ^1 (u/(u^2 +1))ln(1+u^2 )du−2∫_0 ^1 ((ulnu)/(u^2 +1))du also by parts ∫_0 ^1 (u/(u^2 +1))ln(1+u^2 )du =[(1/2)ln^2 (1+u^2 )]_0 ^1 −∫_0 ^1 (1/2)ln(1+u^2 ).((2u)/(1+u^2 )) =(1/2)ln^2 (2)−∫_0 ^1 (u/(1+u^2 ))ln(1+u^2 )du ⇒∫_0 ^1 ((uln(1+u^2 ))/(u^2 +1))du=(1/4)ln^2 (2) ∫_0 ^1 ((ulnu)/(u^2 +1))du =[(1/2)ln(1+u^2 )lnu]_0 ^1 −(1/2)∫_0 ^1 ln(1+u^2 )(du/u) =−(1/2)∫_0 ^1 ((ln(1+u^2 ))/u)du we have ln(1+x)=Σ_(n=1) ^∞ (−1)^(n−1) (x^n /n) ⇒ln(1+u^2 )=Σ_(n=1) ^∞ (−1)^(n−1) (u^(2n) /n) ⇒∫_0 ^1 ((ln(1+u^2 ))/u)du =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^1 u^(2n−1) du =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)[(1/(2n))u^(2n) ]_0 ^(1 ) =(1/2)Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) ⇒ ∫_0 ^1 ((ulnu)/(1+u^2 ))du =(1/4)Σ_(n=1) ^∞ (((−1)^n )/n^2 )=(1/4)(2^(1−2) −1)ξ(2) =(1/4)(−(1/2))ξ(2) =−(1/8).(π^2 /6) =−(π^2 /(48)) ⇒ ϕ^′ (a) =−(1/(2a)){(1/4)ln^2 (2)+(π^2 /(24))} ⇒ ϕ(a)=−((1/8)ln^2 2+(π^2 /(48)))lna +C ⇒ϕ(1)=C rest to find C!! be continued...](https://www.tinkutara.com/question/Q131627.png)
$$\Phi\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{ln}\left(\mathrm{sinx}\right).\mathrm{ln}\left(\mathrm{cosx}\right)}{\mathrm{tanx}}\mathrm{dx}\:\mathrm{let}\:\varphi\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{ln}\left(\mathrm{asinx}\right)\mathrm{ln}\left(\mathrm{cosx}\right)}{\mathrm{tanx}}\mathrm{dx}\:\Rightarrow \\ $$$$\varphi^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sinx}}{\mathrm{asinx}}.\frac{\mathrm{ln}\left(\mathrm{cosx}\right)}{\mathrm{tanx}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{ln}\left(\mathrm{cosx}\right)}{\mathrm{tanx}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{ln}\left(\sqrt{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}}\right)}{\mathrm{tanx}}\mathrm{dx}\:=_{\mathrm{tanx}=\mathrm{t}} \:\:\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\right)}{\mathrm{t}}×\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2a}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{t}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{dt}\:\mathrm{and}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{t}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(…\right)\mathrm{dt}\:+\int_{\mathrm{1}} ^{\infty} \left(..\sqrt{\left.\right)\mathrm{dt}}\right. \\ $$$$\int_{\mathrm{1}} ^{\infty} \left(…\right)\mathrm{dt}\:=_{\mathrm{t}=\frac{\mathrm{1}}{\mathrm{u}}} \:\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{u}\frac{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }\right)}{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }\right)}\left(−\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} }\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{u}\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)−\mathrm{2lnu}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{du}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{u}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\mathrm{du}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ulnu}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{du} \\ $$$$\mathrm{also}\:\mathrm{by}\:\mathrm{parts}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{u}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\mathrm{du} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right).\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\mathrm{du}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{uln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}\mathrm{du}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ulnu}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{du}\:=\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\mathrm{lnu}\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\frac{\mathrm{du}}{\mathrm{u}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}{\mathrm{u}}\mathrm{du}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \frac{\mathrm{u}^{\mathrm{2n}} }{\mathrm{n}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}{\mathrm{u}}\mathrm{du}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{u}^{\mathrm{2n}−\mathrm{1}} \mathrm{du} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\left[\frac{\mathrm{1}}{\mathrm{2n}}\mathrm{u}^{\mathrm{2n}} \right]_{\mathrm{0}} ^{\mathrm{1}\:} =\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ulnu}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{4}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\xi\left(\mathrm{2}\right)\:=−\frac{\mathrm{1}}{\mathrm{8}}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{48}}\:\Rightarrow \\ $$$$\varphi^{'} \left(\mathrm{a}\right)\:=−\frac{\mathrm{1}}{\mathrm{2a}}\left\{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{24}}\right\}\:\Rightarrow \\ $$$$\varphi\left(\mathrm{a}\right)=−\left(\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}^{\mathrm{2}} \mathrm{2}+\frac{\pi^{\mathrm{2}} }{\mathrm{48}}\right)\mathrm{lna}\:+\mathrm{C}\:\Rightarrow\varphi\left(\mathrm{1}\right)=\mathrm{C}\:\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{C}!!\:\:\mathrm{be}\:\mathrm{continued}… \\ $$
