Question Number 6715 by Tawakalitu. last updated on 15/Jul/16
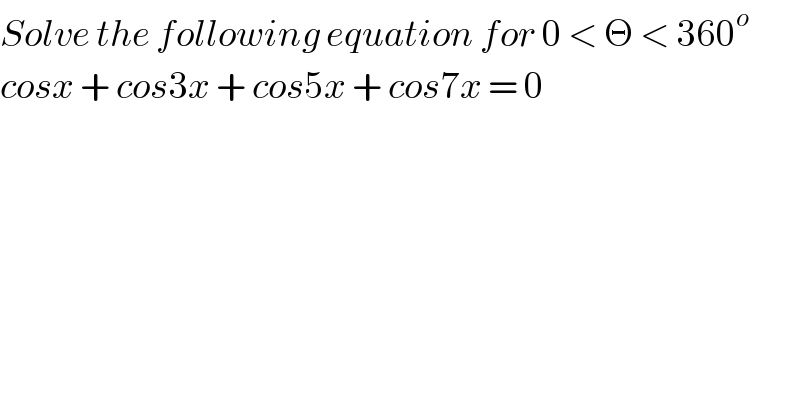
$${Solve}\:{the}\:{following}\:{equation}\:{for}\:\mathrm{0}\:<\:\Theta\:<\:\mathrm{360}^{{o}} \\ $$$${cosx}\:+\:{cos}\mathrm{3}{x}\:+\:{cos}\mathrm{5}{x}\:+\:{cos}\mathrm{7}{x}\:=\:\mathrm{0} \\ $$
Answered by Yozzii last updated on 16/Jul/16
![We know the identity cosa+cosb=2cos((a+b)/2)cos((a−b)/2) for a,b∈R....(1) Let u=cosx+cos3x+cos5x+cos7x. From (1): cosx+cos7x=2cos4xcos3x cos5x+cos3x=2cos4xcosx ∴u=2cos4x(cos3x+cosx) u=2cos4x(2cos2xcosx) u=4cosxcos2xcos4x. u=0⇒cosxcos2xcos4x=0.....(2) (2) is true if (i) cosx=0⇒x=2nπ±0.5π (n∈Z) or (ii) cos2x=0⇒x=mπ±0.25π (m∈Z) or (iii) cos4x=0⇒x=0.5kπ±0.125π (k∈Z) −−−−−−−−−−−−−−−−−−−−−− Since x∈[0,2π], (i) gives x=0.5π,1.5π; (ii) gives x=0.25π,0.75π,1.25π,1.75π; and (iii) gives x=0.125π,0.625π,0.375π,0.875π,1.125π,1.375π,1.625π,1.875π −−−−−−−−−−−−−−−−−−−−−−−− In summary, the solution set for u=0 is {0.125π,0.25π,0.375π,0.5π,0.625π,0.75π,0.875π, 1.125π,1.25π,1.375π,1.5π,1.625π,1.75π,1.875π}](https://www.tinkutara.com/question/Q6717.png)
$${We}\:{know}\:{the}\:{identity}\:{cosa}+{cosb}=\mathrm{2}{cos}\frac{{a}+{b}}{\mathrm{2}}{cos}\frac{{a}−{b}}{\mathrm{2}}\:{for}\:{a},{b}\in\mathbb{R}….\left(\mathrm{1}\right) \\ $$$${Let}\:{u}={cosx}+{cos}\mathrm{3}{x}+{cos}\mathrm{5}{x}+{cos}\mathrm{7}{x}. \\ $$$${From}\:\left(\mathrm{1}\right): \\ $$$${cosx}+{cos}\mathrm{7}{x}=\mathrm{2}{cos}\mathrm{4}{xcos}\mathrm{3}{x} \\ $$$${cos}\mathrm{5}{x}+{cos}\mathrm{3}{x}=\mathrm{2}{cos}\mathrm{4}{xcosx} \\ $$$$ \\ $$$$\therefore{u}=\mathrm{2}{cos}\mathrm{4}{x}\left({cos}\mathrm{3}{x}+{cosx}\right) \\ $$$${u}=\mathrm{2}{cos}\mathrm{4}{x}\left(\mathrm{2}{cos}\mathrm{2}{xcosx}\right) \\ $$$${u}=\mathrm{4}{cosxcos}\mathrm{2}{xcos}\mathrm{4}{x}. \\ $$$${u}=\mathrm{0}\Rightarrow{cosxcos}\mathrm{2}{xcos}\mathrm{4}{x}=\mathrm{0}…..\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{2}\right)\:{is}\:{true}\:{if}\: \\ $$$$\left({i}\right)\:{cosx}=\mathrm{0}\Rightarrow{x}=\mathrm{2}{n}\pi\pm\mathrm{0}.\mathrm{5}\pi\:\:\:\left({n}\in\mathbb{Z}\right) \\ $$$${or} \\ $$$$\left({ii}\right)\:{cos}\mathrm{2}{x}=\mathrm{0}\Rightarrow{x}={m}\pi\pm\mathrm{0}.\mathrm{25}\pi\:\:\:\left({m}\in\mathbb{Z}\right) \\ $$$${or} \\ $$$$\left({iii}\right)\:{cos}\mathrm{4}{x}=\mathrm{0}\Rightarrow{x}=\mathrm{0}.\mathrm{5}{k}\pi\pm\mathrm{0}.\mathrm{125}\pi\:\:\left({k}\in\mathbb{Z}\right) \\ $$$$−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Since}\:{x}\in\left[\mathrm{0},\mathrm{2}\pi\right],\:\left({i}\right)\:{gives}\:{x}=\mathrm{0}.\mathrm{5}\pi,\mathrm{1}.\mathrm{5}\pi; \\ $$$$\left({ii}\right)\:{gives}\:{x}=\mathrm{0}.\mathrm{25}\pi,\mathrm{0}.\mathrm{75}\pi,\mathrm{1}.\mathrm{25}\pi,\mathrm{1}.\mathrm{75}\pi; \\ $$$$\:{and}\:\left({iii}\right)\:{gives}\:{x}=\mathrm{0}.\mathrm{125}\pi,\mathrm{0}.\mathrm{625}\pi,\mathrm{0}.\mathrm{375}\pi,\mathrm{0}.\mathrm{875}\pi,\mathrm{1}.\mathrm{125}\pi,\mathrm{1}.\mathrm{375}\pi,\mathrm{1}.\mathrm{625}\pi,\mathrm{1}.\mathrm{875}\pi \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${In}\:{summary},\:{the}\:{solution}\:{set}\:{for}\:{u}=\mathrm{0}\:{is} \\ $$$$\left\{\mathrm{0}.\mathrm{125}\pi,\mathrm{0}.\mathrm{25}\pi,\mathrm{0}.\mathrm{375}\pi,\mathrm{0}.\mathrm{5}\pi,\mathrm{0}.\mathrm{625}\pi,\mathrm{0}.\mathrm{75}\pi,\mathrm{0}.\mathrm{875}\pi,\right. \\ $$$$\left.\mathrm{1}.\mathrm{125}\pi,\mathrm{1}.\mathrm{25}\pi,\mathrm{1}.\mathrm{375}\pi,\mathrm{1}.\mathrm{5}\pi,\mathrm{1}.\mathrm{625}\pi,\mathrm{1}.\mathrm{75}\pi,\mathrm{1}.\mathrm{875}\pi\right\} \\ $$
Commented by Tawakalitu. last updated on 16/Jul/16

$${Thanks}\:{so}\:{much} \\ $$
