Question Number 72250 by aliesam last updated on 26/Oct/19
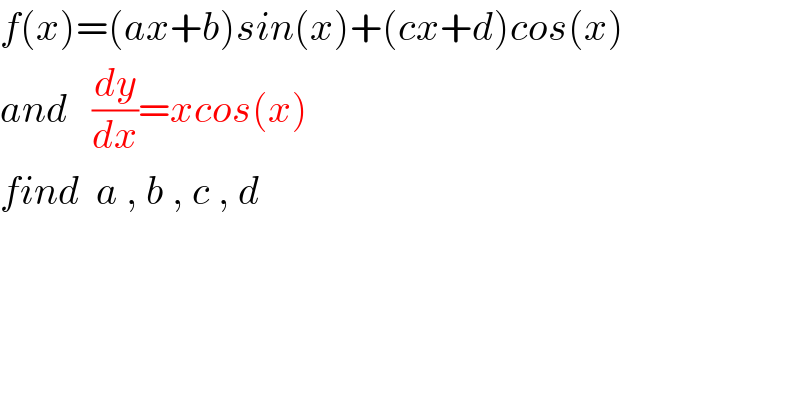
$${f}\left({x}\right)=\left({ax}+{b}\right){sin}\left({x}\right)+\left({cx}+{d}\right){cos}\left({x}\right) \\ $$$${and}\:\:\:\frac{{dy}}{{dx}}={xcos}\left({x}\right) \\ $$$${find}\:\:{a}\:,\:{b}\:,\:{c}\:,\:{d} \\ $$$$ \\ $$$$ \\ $$
Commented by kaivan.ahmadi last updated on 27/Oct/19
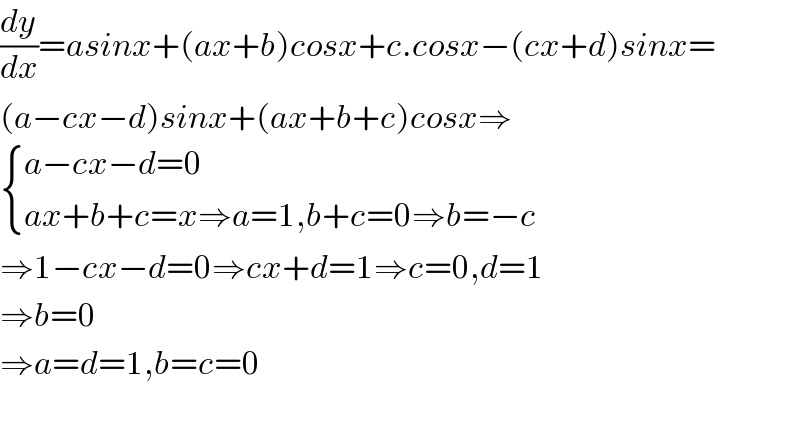
$$\frac{{dy}}{{dx}}={asinx}+\left({ax}+{b}\right){cosx}+{c}.{cosx}−\left({cx}+{d}\right){sinx}= \\ $$$$\left({a}−{cx}−{d}\right){sinx}+\left({ax}+{b}+{c}\right){cosx}\Rightarrow \\ $$$$\begin{cases}{{a}−{cx}−{d}=\mathrm{0}}\\{{ax}+{b}+{c}={x}\Rightarrow{a}=\mathrm{1},{b}+{c}=\mathrm{0}\Rightarrow{b}=−{c}}\end{cases} \\ $$$$\Rightarrow\mathrm{1}−{cx}−{d}=\mathrm{0}\Rightarrow{cx}+{d}=\mathrm{1}\Rightarrow{c}=\mathrm{0},{d}=\mathrm{1} \\ $$$$\Rightarrow{b}=\mathrm{0} \\ $$$$\Rightarrow{a}={d}=\mathrm{1},{b}={c}=\mathrm{0} \\ $$$$ \\ $$
Commented by kaivan.ahmadi last updated on 27/Oct/19

$${f}\left({x}\right)={xsinx}+{cosx} \\ $$$$ \\ $$
