Menu Close

0-sin-x-sin-x-2-x-pi-4-0-cos-x-cos-x-2-x-dx-2-

Tinku Tara 0 Comments
Pin




Question Number 137837 by Ñï= last updated on 07/Apr/21
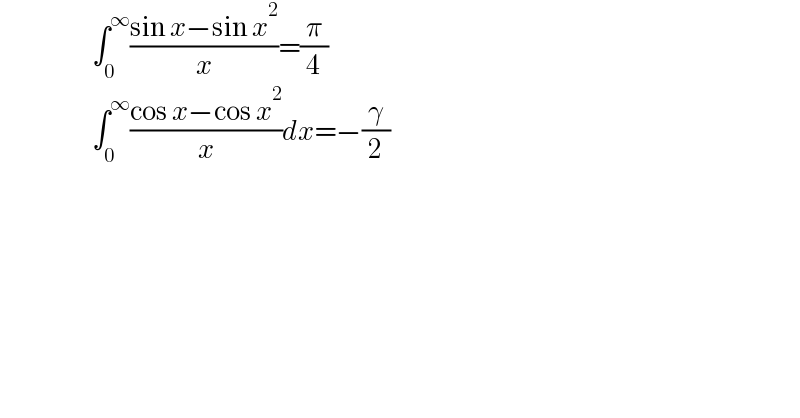
∫_0 ^∞ ((sin x−sin x^2 )/x)=(π/4) ∫_0 ^∞ ((cos x−cos x^2 )/x)dx=−(γ/2)
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\:{x}−\mathrm{sin}\:{x}^{\mathrm{2}} }{{x}}=\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cos}\:{x}−\mathrm{cos}\:{x}^{\mathrm{2}} }{{x}}{dx}=−\frac{\gamma}{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 07/Apr/21
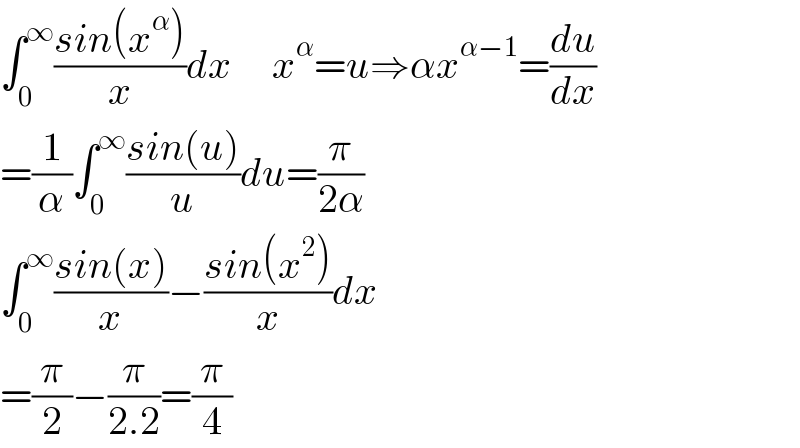
∫_0 ^∞ ((sin(x^α ))/x)dx x^α =u⇒αx^(α−1) =(du/dx) =(1/α)∫_0 ^∞ ((sin(u))/u)du=(π/(2α)) ∫_0 ^∞ ((sin(x))/x)−((sin(x^2 ))/x)dx =(π/2)−(π/(2.2))=(π/4)
$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}^{\alpha} \right)}{{x}}{dx}\:\:\:\:\:{x}^{\alpha} ={u}\Rightarrow\alpha{x}^{\alpha−\mathrm{1}} =\frac{{du}}{{dx}} \\ $$$$=\frac{\mathrm{1}}{\alpha}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({u}\right)}{{u}}{du}=\frac{\pi}{\mathrm{2}\alpha} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right)}{{x}}−\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}}{dx} \\ $$$$=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}.\mathrm{2}}=\frac{\pi}{\mathrm{4}} \\ $$
Answered by mnjuly1970 last updated on 07/Apr/21
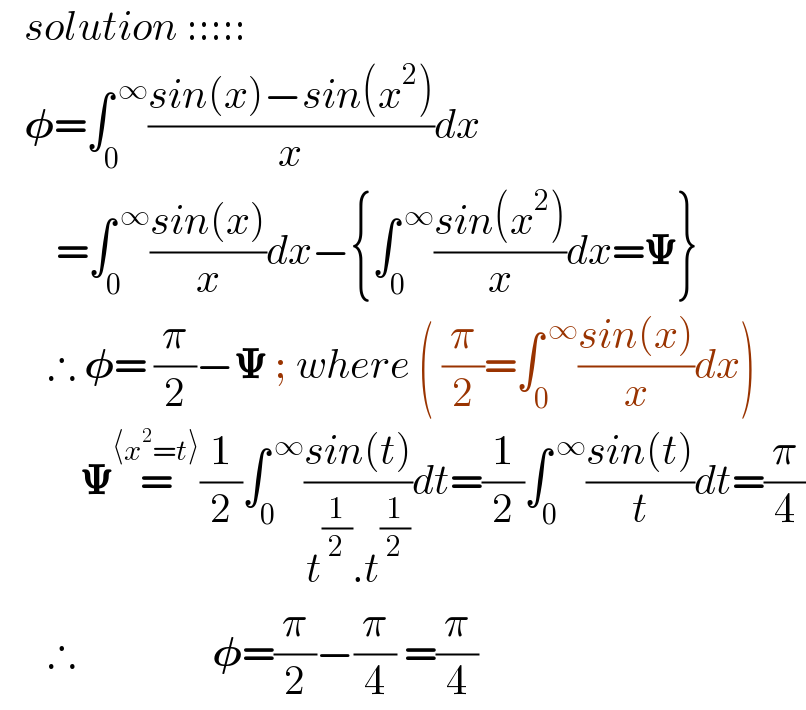
solution ::::: 𝛗=∫_0 ^( ∞) ((sin(x)−sin(x^2 ))/x)dx =∫_0 ^( ∞) ((sin(x))/x)dx−{∫_0 ^( ∞) ((sin(x^2 ))/x)dx=𝚿} ∴ 𝛗= (π/2)−𝚿 ; where ( (π/2)=∫_0 ^( ∞) ((sin(x))/x)dx) 𝚿=^(⟨x^2 =t⟩) (1/2)∫_0 ^( ∞) ((sin(t))/(t^(1/2) .t^(1/2) ))dt=(1/2)∫_0 ^( ∞) ((sin(t))/t)dt=(π/4) ∴ 𝛗=(π/2)−(π/4) =(π/4)
$$\:\:\:{solution}\:::::: \\ $$$$\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({x}\right)−{sin}\left({x}^{\mathrm{2}} \right)}{{x}}{dx} \\ $$$$\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({x}\right)}{{x}}{dx}−\left\{\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}}{dx}=\boldsymbol{\Psi}\right\} \\ $$$$\:\:\:\:\:\:\therefore\:\boldsymbol{\phi}=\:\frac{\pi}{\mathrm{2}}−\boldsymbol{\Psi}\:;\:{where}\:\left(\:\frac{\pi}{\mathrm{2}}=\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({x}\right)}{{x}}{dx}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\boldsymbol{\Psi}\overset{\langle{x}^{\mathrm{2}} ={t}\rangle} {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({t}\right)}{{t}^{\frac{\mathrm{1}}{\mathrm{2}}} .{t}^{\frac{\mathrm{1}}{\mathrm{2}}} }{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({t}\right)}{{t}}{dt}=\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\therefore\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\phi}=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\:=\frac{\pi}{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 08/Apr/21
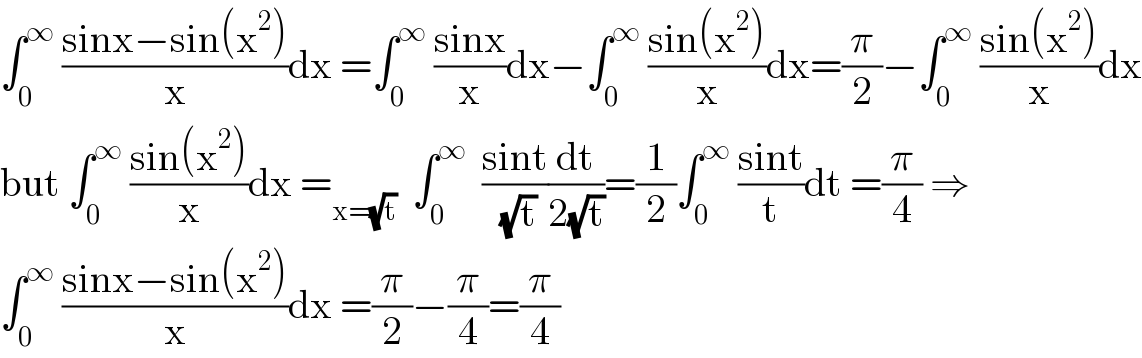
∫_0 ^∞ ((sinx−sin(x^2 ))/x)dx =∫_0 ^∞ ((sinx)/x)dx−∫_0 ^∞ ((sin(x^2 ))/x)dx=(π/2)−∫_0 ^∞ ((sin(x^2 ))/x)dx but ∫_0 ^∞ ((sin(x^2 ))/x)dx =_(x=(√t)) ∫_0 ^∞ ((sint)/( (√t)))(dt/(2(√t)))=(1/2)∫_0 ^∞ ((sint)/t)dt =(π/4) ⇒ ∫_0 ^∞ ((sinx−sin(x^2 ))/x)dx =(π/2)−(π/4)=(π/4)
$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sinx}−\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sinx}}{\mathrm{x}}\mathrm{dx}−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}}\mathrm{dx}=\frac{\pi}{\mathrm{2}}−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{but}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}}\mathrm{dx}\:=_{\mathrm{x}=\sqrt{\mathrm{t}}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{sint}}{\:\sqrt{\mathrm{t}}}\frac{\mathrm{dt}}{\mathrm{2}\sqrt{\mathrm{t}}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sint}}{\mathrm{t}}\mathrm{dt}\:=\frac{\pi}{\mathrm{4}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sinx}−\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}}\mathrm{dx}\:=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 08/Apr/21
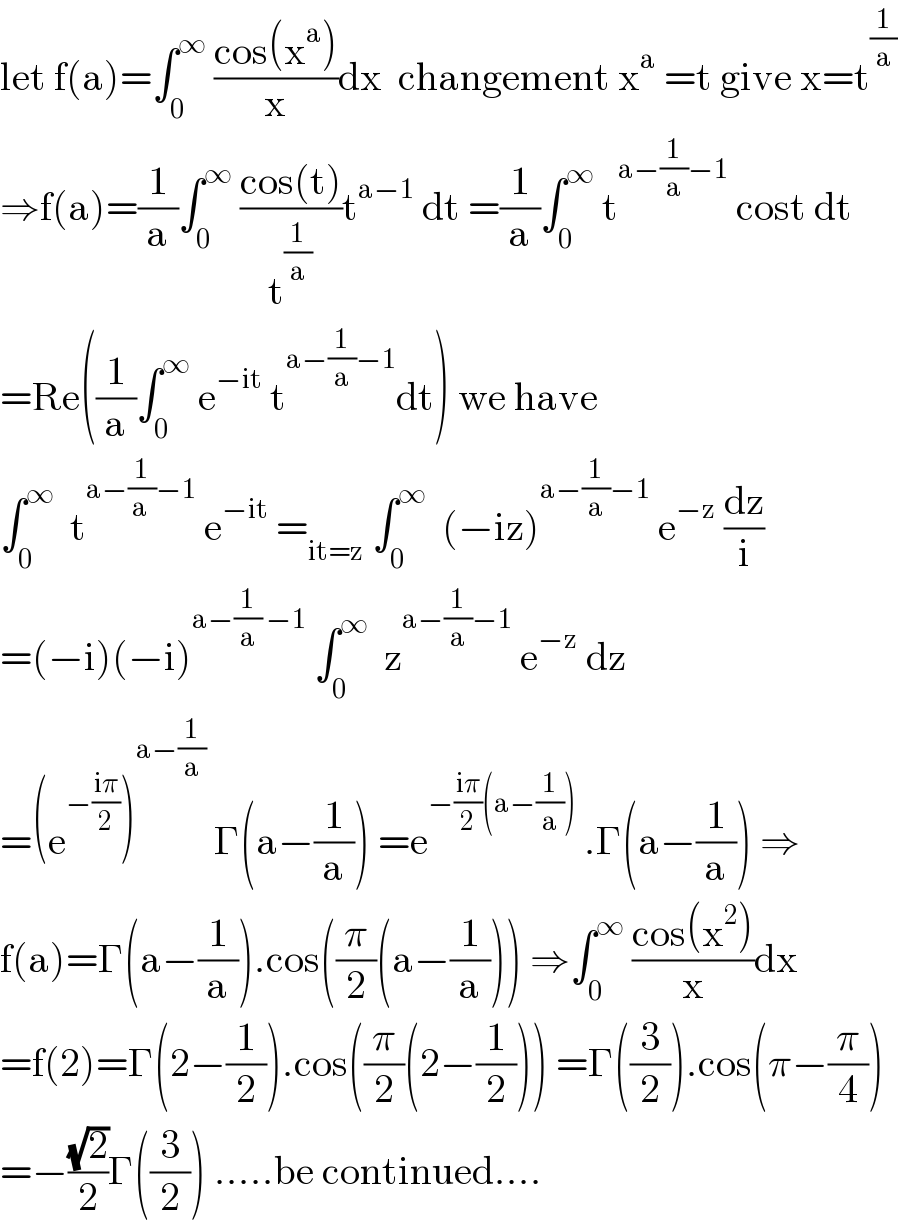
let f(a)=∫_0 ^∞ ((cos(x^a ))/x)dx changement x^a =t give x=t^(1/a) ⇒f(a)=(1/a)∫_0 ^∞ ((cos(t))/t^(1/a) )t^(a−1) dt =(1/a)∫_0 ^∞ t^(a−(1/a)−1) cost dt =Re((1/a)∫_0 ^∞ e^(−it) t^(a−(1/a)−1) dt) we have ∫_0 ^∞ t^(a−(1/(a ))−1) e^(−it) =_(it=z) ∫_0 ^∞ (−iz)^(a−(1/a)−1) e^(−z) (dz/i) =(−i)(−i)^(a−(1/a) −1) ∫_0 ^∞ z^(a−(1/a)−1) e^(−z) dz =(e^(−((iπ)/2)) )^(a−(1/a)) Γ(a−(1/a)) =e^(−((iπ)/2)(a−(1/a))) .Γ(a−(1/a)) ⇒ f(a)=Γ(a−(1/a)).cos((π/2)(a−(1/a))) ⇒∫_0 ^∞ ((cos(x^2 ))/x)dx =f(2)=Γ(2−(1/2)).cos((π/2)(2−(1/2))) =Γ((3/2)).cos(π−(π/4)) =−((√2)/2)Γ((3/2)) .....be continued....
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{x}^{\mathrm{a}} \right)}{\mathrm{x}}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}^{\mathrm{a}} \:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{a}}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{t}\right)}{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{a}}} }\mathrm{t}^{\mathrm{a}−\mathrm{1}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}−\mathrm{1}} \:\mathrm{cost}\:\mathrm{dt} \\ $$$$=\mathrm{Re}\left(\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{it}} \:\mathrm{t}^{\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}−\mathrm{1}} \mathrm{dt}\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{t}^{\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}\:}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{it}} \:=_{\mathrm{it}=\mathrm{z}} \:\int_{\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{iz}\right)^{\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{z}} \:\frac{\mathrm{dz}}{\mathrm{i}} \\ $$$$=\left(−\mathrm{i}\right)\left(−\mathrm{i}\right)^{\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}\:−\mathrm{1}} \:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{z}^{\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{z}} \:\mathrm{dz} \\ $$$$=\left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)^{\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}} \:\Gamma\left(\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}\right)\:=\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}\left(\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}\right)} \:.\Gamma\left(\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\Gamma\left(\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}\right).\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\left(\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}\right)\right)\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{f}\left(\mathrm{2}\right)=\Gamma\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\right).\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\:=\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right).\mathrm{cos}\left(\pi−\frac{\pi}{\mathrm{4}}\right) \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:…..\mathrm{be}\:\mathrm{continued}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *