Question Number 545 by 123456 last updated on 25/Jan/15
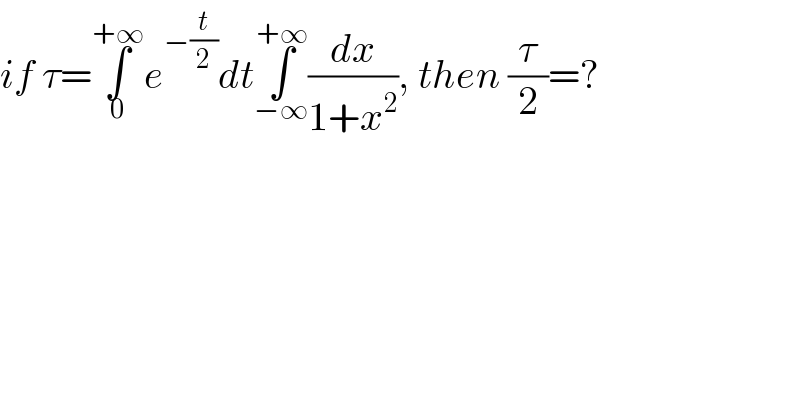
$${if}\:\tau=\underset{\mathrm{0}} {\overset{+\infty} {\int}}{e}^{−\frac{{t}}{\mathrm{2}}} {dt}\underset{−\infty} {\overset{+\infty} {\int}}\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} },\:{then}\:\frac{\tau}{\mathrm{2}}=? \\ $$
Answered by prakash jain last updated on 24/Jan/15
![∫_(−∞) ^(+∞) (dx/(1+x^2 ))=[tan^(−1) x]_(−∞) ^(+∞) =π ∫_0 ^(+∞) e^(−(t/2)) dt=[−2e^(−(t/2)) ]_0 ^∞ =2 τ=2π (τ/2)=π](https://www.tinkutara.com/question/Q549.png)
$$\underset{−\infty} {\overset{+\infty} {\int}}\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }=\left[\mathrm{tan}^{−\mathrm{1}} {x}\right]_{−\infty} ^{+\infty} =\pi \\ $$$$\underset{\mathrm{0}} {\overset{+\infty} {\int}}{e}^{−\frac{{t}}{\mathrm{2}}} {dt}=\left[−\mathrm{2}{e}^{−\frac{{t}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\infty} =\mathrm{2} \\ $$$$\tau=\mathrm{2}\pi \\ $$$$\frac{\tau}{\mathrm{2}}=\pi \\ $$
