Question Number 72392 by mathmax by abdo last updated on 28/Oct/19
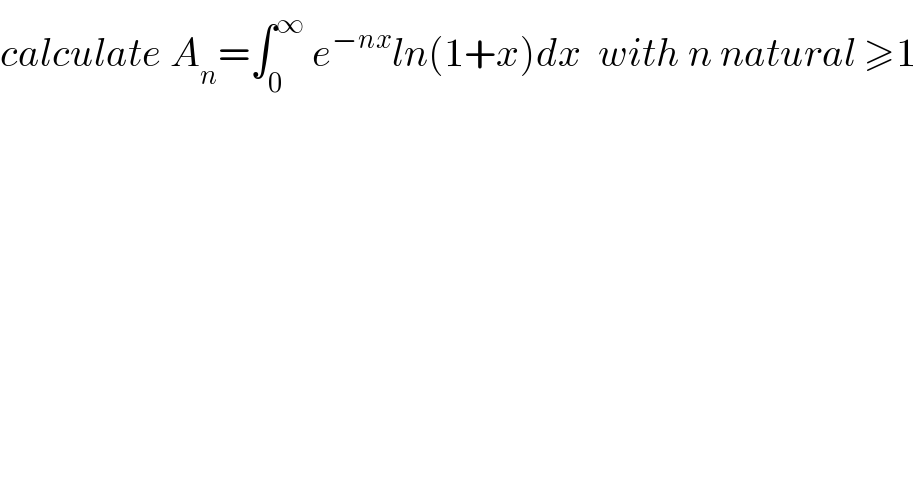
$${calculate}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{e}^{−{nx}} {ln}\left(\mathrm{1}+{x}\right){dx}\:\:{with}\:{n}\:{natural}\:\geqslant\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 07/Nov/19
![A_n =∫_0 ^∞ e^(−nx) ln(1+x)dx =_(1+x=t) ∫_1 ^(+∞) e^(−n(t−1)) lnt dt =e^n ∫_1 ^(+∞) e^(−nt) ln(t)dt =_(nt=u) e^n ∫_n ^(+∞) e^(−u) ln((u/n))(du/n) =(e^n /n) ∫_n ^(+∞) e^(−u) {lnu−ln(n)}du =(e^n /n)∫_n ^(+∞) e^(−u) ln(u)−((e^n ln(n))/n) ∫_n ^(+∞) e^(−u) du =(e^n /n) (∫_n ^0 e^(−u) ln(u)du+∫_0 ^∞ e^(−u) lnudu)−((e^n ln(n))/n)[−e^(−u) ]_n ^(+∞) =(e^n /n){−γ−∫_0 ^n e^(−u) lnu du}−((e^n ln(n))/n)×e^(−n) =−γ (e^n /n)−(e^n /n) ∫_0 ^n e^(−u) lnu du −((ln(n))/n) ....be continued....](https://www.tinkutara.com/question/Q73158.png)
$${A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{e}^{−{nx}} {ln}\left(\mathrm{1}+{x}\right){dx}\:=_{\mathrm{1}+{x}={t}} \:\:\int_{\mathrm{1}} ^{+\infty} \:{e}^{−{n}\left({t}−\mathrm{1}\right)} {lnt}\:{dt} \\ $$$$={e}^{{n}} \:\int_{\mathrm{1}} ^{+\infty} \:{e}^{−{nt}} {ln}\left({t}\right){dt}\:=_{{nt}={u}} \:\:{e}^{{n}} \:\int_{{n}} ^{+\infty} \:{e}^{−{u}} {ln}\left(\frac{{u}}{{n}}\right)\frac{{du}}{{n}} \\ $$$$=\frac{{e}^{{n}} }{{n}}\:\int_{{n}} ^{+\infty} \:{e}^{−{u}} \left\{{lnu}−{ln}\left({n}\right)\right\}{du} \\ $$$$=\frac{{e}^{{n}} }{{n}}\int_{{n}} ^{+\infty} \:{e}^{−{u}} {ln}\left({u}\right)−\frac{{e}^{{n}} {ln}\left({n}\right)}{{n}}\:\int_{{n}} ^{+\infty} {e}^{−{u}} \:{du} \\ $$$$=\frac{{e}^{{n}} }{{n}}\:\left(\int_{{n}} ^{\mathrm{0}} \:{e}^{−{u}} {ln}\left({u}\right){du}+\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}} \:{lnudu}\right)−\frac{{e}^{{n}} {ln}\left({n}\right)}{{n}}\left[−{e}^{−{u}} \right]_{{n}} ^{+\infty} \\ $$$$=\frac{{e}^{{n}} }{{n}}\left\{−\gamma−\int_{\mathrm{0}} ^{{n}} \:{e}^{−{u}} {lnu}\:{du}\right\}−\frac{{e}^{{n}} {ln}\left({n}\right)}{{n}}×{e}^{−{n}} \\ $$$$=−\gamma\:\frac{{e}^{{n}} }{{n}}−\frac{{e}^{{n}} }{{n}}\:\int_{\mathrm{0}} ^{{n}} \:{e}^{−{u}} {lnu}\:{du}\:−\frac{{ln}\left({n}\right)}{{n}}\:….{be}\:{continued}…. \\ $$
