Question Number 6872 by hanandmishra026@gmail.com last updated on 31/Jul/16
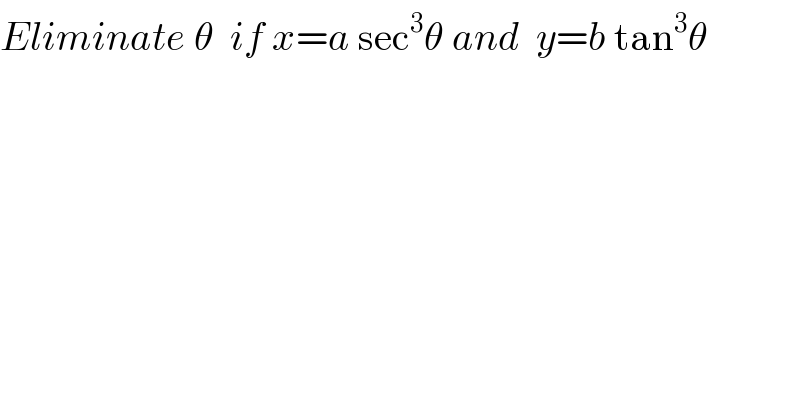
$${Eliminate}\:\theta\:\:{if}\:{x}={a}\:\mathrm{sec}^{\mathrm{3}} \theta\:{and}\:\:{y}={b}\:\mathrm{tan}^{\mathrm{3}} \theta \\ $$
Commented by Yozzii last updated on 31/Jul/16
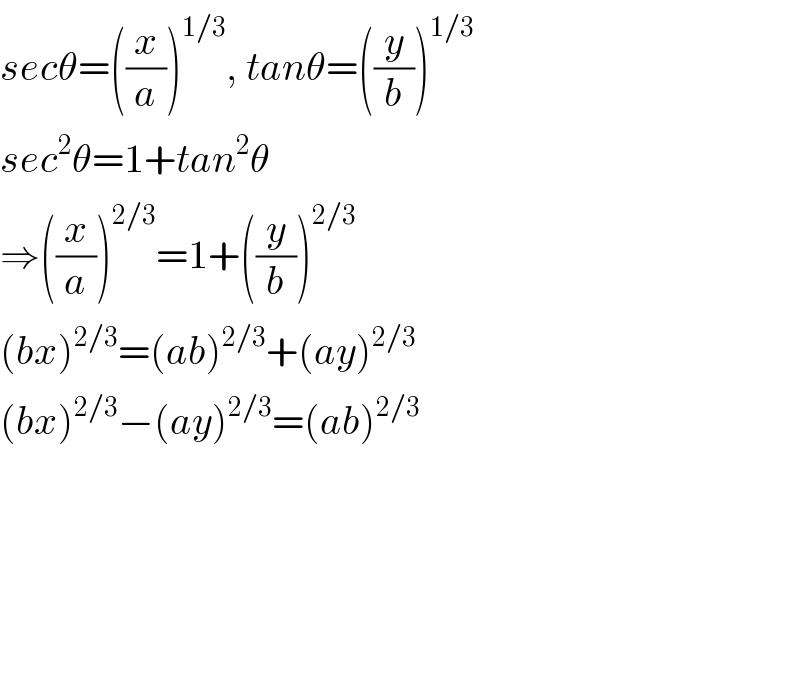
$${sec}\theta=\left(\frac{{x}}{{a}}\right)^{\mathrm{1}/\mathrm{3}} ,\:{tan}\theta=\left(\frac{{y}}{{b}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$${sec}^{\mathrm{2}} \theta=\mathrm{1}+{tan}^{\mathrm{2}} \theta \\ $$$$\Rightarrow\left(\frac{{x}}{{a}}\right)^{\mathrm{2}/\mathrm{3}} =\mathrm{1}+\left(\frac{{y}}{{b}}\right)^{\mathrm{2}/\mathrm{3}} \\ $$$$\left({bx}\right)^{\mathrm{2}/\mathrm{3}} =\left({ab}\right)^{\mathrm{2}/\mathrm{3}} +\left({ay}\right)^{\mathrm{2}/\mathrm{3}} \\ $$$$\left({bx}\right)^{\mathrm{2}/\mathrm{3}} −\left({ay}\right)^{\mathrm{2}/\mathrm{3}} =\left({ab}\right)^{\mathrm{2}/\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
