Question Number 137946 by otchereabdullai@gmail.com last updated on 08/Apr/21

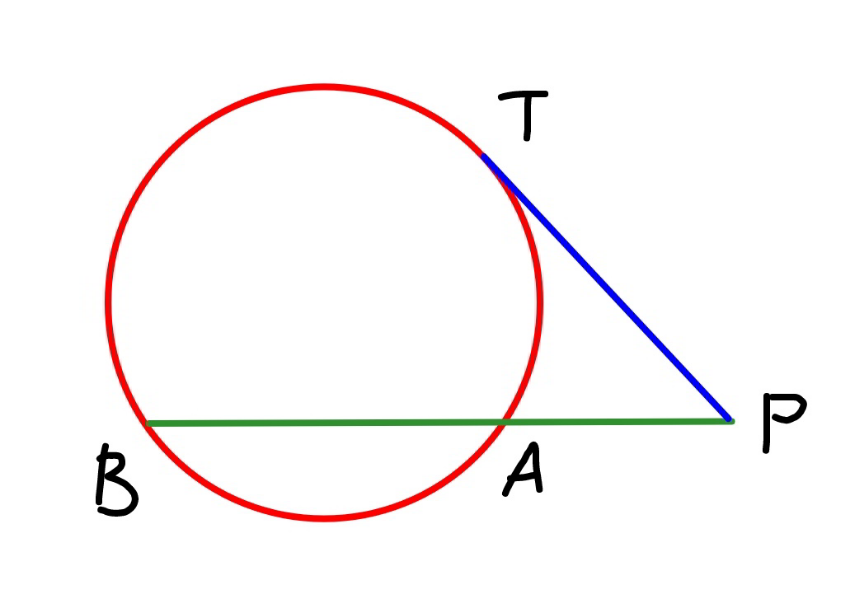
$$\mathrm{From}\:\mathrm{a}\:\mathrm{poin}\:\mathrm{P}\:\mathrm{outside}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{a} \\ $$$$\mathrm{tangent}\:\mathrm{is}\:\mathrm{drawn}\:\mathrm{to}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{at}\:\mathrm{T}. \\ $$$$\mathrm{from}\:\mathrm{P}\:\mathrm{a}\:\mathrm{line}\:\mathrm{is}\:\mathrm{drawn}\:\mathrm{to}\:\mathrm{circle}\:\mathrm{at} \\ $$$$\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:.\:\mathrm{Find}\:\mathrm{lenth}\:\mathrm{PT}\:\mathrm{giving}\:\mathrm{that} \\ $$$$\mathrm{i}.\:\mathrm{PA}\:=\mathrm{6} \\ $$$$\:\:\:\:\mathrm{AB}=\mathrm{8} \\ $$$$\mathrm{ii}.\:\mathrm{PB}=\mathrm{18} \\ $$$$\:\:\:\:\:\mathrm{PT}=\mathrm{12} \\ $$
Commented by mr W last updated on 08/Apr/21
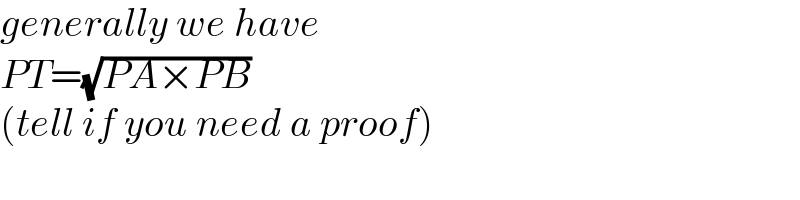
$${generally}\:{we}\:{have} \\ $$$${PT}=\sqrt{{PA}×{PB}} \\ $$$$\left({tell}\:{if}\:{you}\:{need}\:{a}\:{proof}\right) \\ $$
Commented by mr W last updated on 08/Apr/21
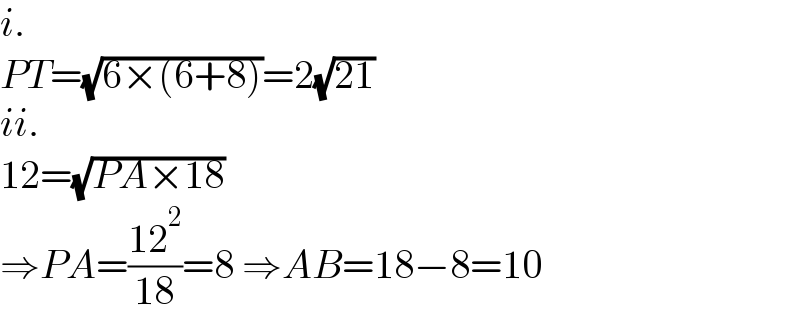
$${i}. \\ $$$${PT}=\sqrt{\mathrm{6}×\left(\mathrm{6}+\mathrm{8}\right)}=\mathrm{2}\sqrt{\mathrm{21}} \\ $$$${ii}. \\ $$$$\mathrm{12}=\sqrt{{PA}×\mathrm{18}} \\ $$$$\Rightarrow{PA}=\frac{\mathrm{12}^{\mathrm{2}} }{\mathrm{18}}=\mathrm{8}\:\Rightarrow{AB}=\mathrm{18}−\mathrm{8}=\mathrm{10} \\ $$
Commented by mr W last updated on 08/Apr/21
Commented by otchereabdullai@gmail.com last updated on 08/Apr/21
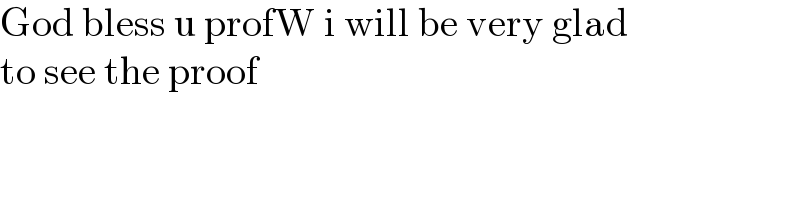
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{u}\:\mathrm{profW}\:\mathrm{i}\:\mathrm{will}\:\mathrm{be}\:\mathrm{very}\:\mathrm{glad}\: \\ $$$$\mathrm{to}\:\mathrm{see}\:\mathrm{the}\:\mathrm{proof} \\ $$
Commented by mr W last updated on 08/Apr/21
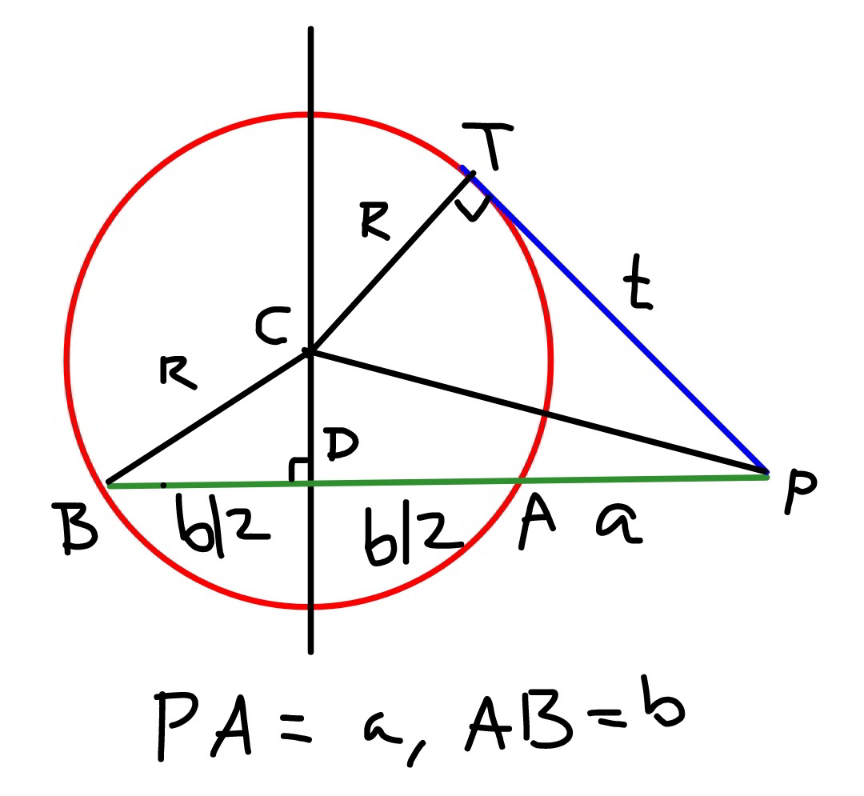
Commented by mr W last updated on 08/Apr/21
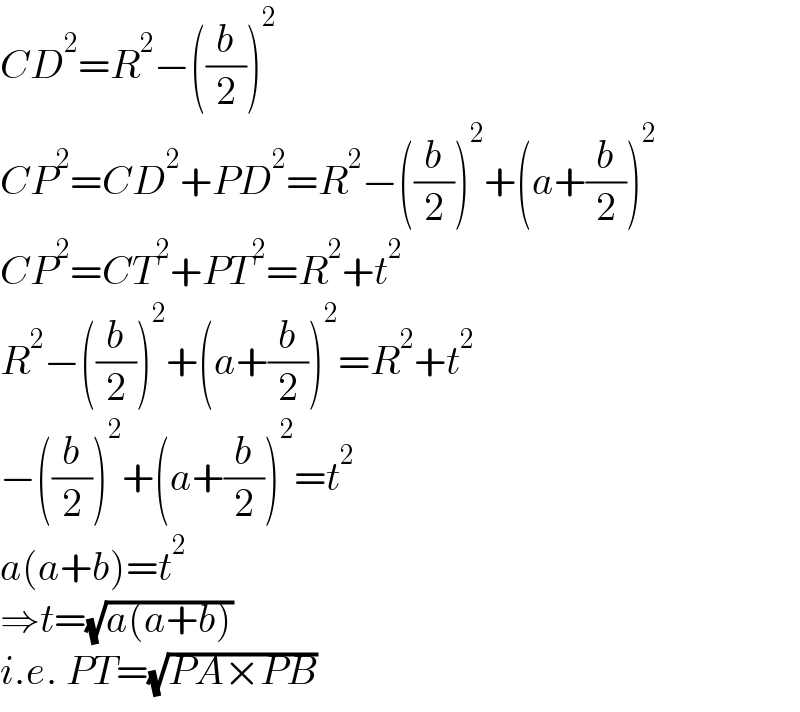
$${CD}^{\mathrm{2}} ={R}^{\mathrm{2}} −\left(\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${CP}^{\mathrm{2}} ={CD}^{\mathrm{2}} +{PD}^{\mathrm{2}} ={R}^{\mathrm{2}} −\left(\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({a}+\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${CP}^{\mathrm{2}} ={CT}^{\mathrm{2}} +{PT}^{\mathrm{2}} ={R}^{\mathrm{2}} +{t}^{\mathrm{2}} \\ $$$${R}^{\mathrm{2}} −\left(\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({a}+\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} +{t}^{\mathrm{2}} \\ $$$$−\left(\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({a}+\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} ={t}^{\mathrm{2}} \\ $$$${a}\left({a}+{b}\right)={t}^{\mathrm{2}} \\ $$$$\Rightarrow{t}=\sqrt{{a}\left({a}+{b}\right)} \\ $$$${i}.{e}.\:{PT}=\sqrt{{PA}×{PB}} \\ $$
Commented by otchereabdullai@gmail.com last updated on 08/Apr/21

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{kindness}\:\mathrm{and}\:\mathrm{may}\:\mathrm{the} \\ $$$$\mathrm{almigthy}\:\mathrm{Allah}\:\:\mathrm{add}\:\mathrm{more}\:\mathrm{years}\:\mathrm{to}\: \\ $$$$\mathrm{age} \\ $$
