Question Number 137953 by mnjuly1970 last updated on 08/Apr/21
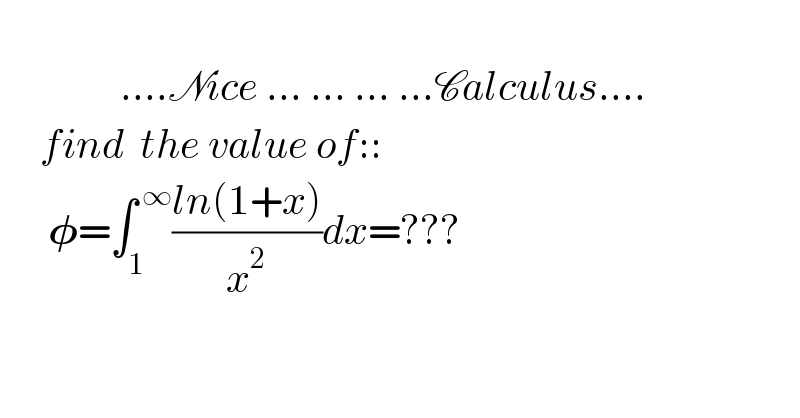
$$\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\mathscr{N}{ice}\:…\:…\:…\:…\mathscr{C}{alculus}…. \\ $$$$\:\:\:\:\:{find}\:\:{the}\:{value}\:{of}:: \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}=\int_{\mathrm{1}} ^{\:\infty} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} }{dx}=??? \\ $$
Answered by ΓΓ―= last updated on 08/Apr/21
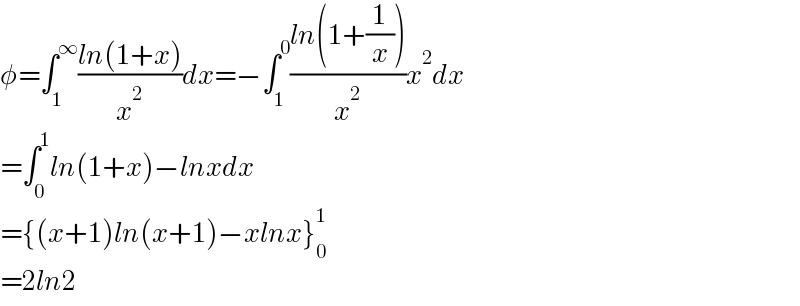
$$\phi=\int_{\mathrm{1}} ^{\infty} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} }{dx}=β\int_{\mathrm{1}} ^{\mathrm{0}} \frac{{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)}{{x}^{\mathrm{2}} }{x}^{\mathrm{2}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}\right)β{lnxdx} \\ $$$$=\left\{\left({x}+\mathrm{1}\right){ln}\left({x}+\mathrm{1}\right)β{xlnx}\right\}_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{2}{ln}\mathrm{2} \\ $$
Commented by mnjuly1970 last updated on 08/Apr/21
$$\:\:{very}\:{nice}\:{solution}…{thank}\:{you} \\ $$$${mr}\:… \\ $$
Answered by mnjuly1970 last updated on 08/Apr/21
![f(a)=β«_1 ^( β) ((ln(1+ax))/x^2 )dx f β²(a)=β«_1 ^( β) (1/(x(1+ax)))dx =β«_1 ^( β) ((1/x) β(a/(1+ax)))dx=[ln((x/(1+ax)))]_1 ^β =βln(a)+ln(1+a) β΄ f(a)=aβaln(a)+(1+a)ln(1+a)β(a)+C f(0)=0=C π=f (1)=1+2ln(2)β1=ln(4) π=ln(4)...β](https://www.tinkutara.com/question/Q137960.png)
$$\:\:\:\:{f}\left({a}\right)=\int_{\mathrm{1}} ^{\:\infty} \frac{{ln}\left(\mathrm{1}+{ax}\right)}{{x}^{\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\:\:\:\:{f}\:'\left({a}\right)=\int_{\mathrm{1}} ^{\:\infty} \frac{\mathrm{1}}{{x}\left(\mathrm{1}+{ax}\right)}{dx} \\ $$$$\:\:\:\:\:\:=\int_{\mathrm{1}} ^{\:\infty} \left(\frac{\mathrm{1}}{{x}}\:β\frac{{a}}{\mathrm{1}+{ax}}\right){dx}=\left[{ln}\left(\frac{{x}}{\mathrm{1}+{ax}}\right)\right]_{\mathrm{1}} ^{\infty} \\ $$$$=β{ln}\left({a}\right)+{ln}\left(\mathrm{1}+{a}\right) \\ $$$$\:\therefore\:{f}\left({a}\right)={a}β{aln}\left({a}\right)+\left(\mathrm{1}+{a}\right){ln}\left(\mathrm{1}+{a}\right)β\left({a}\right)+{C} \\ $$$$\:\:\:{f}\left(\mathrm{0}\right)=\mathrm{0}={C} \\ $$$$\:\:\:\boldsymbol{\phi}={f}\:\left(\mathrm{1}\right)=\mathrm{1}+\mathrm{2}{ln}\left(\mathrm{2}\right)β\mathrm{1}={ln}\left(\mathrm{4}\right) \\ $$$$\:\:\:\:\boldsymbol{\phi}={ln}\left(\mathrm{4}\right)…\checkmark \\ $$