Question Number 204396 by Thierrybadouana last updated on 15/Feb/24
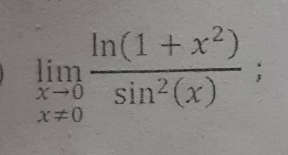
Answered by Faetmaaa last updated on 27/Feb/24
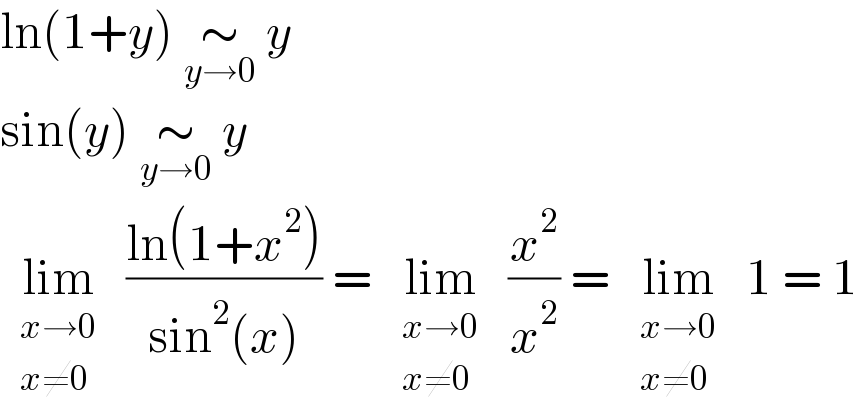
$$\mathrm{ln}\left(\mathrm{1}+{y}\right)\:\underset{{y}\rightarrow\mathrm{0}} {\sim}\:{y} \\ $$$$\mathrm{sin}\left({y}\right)\:\underset{{y}\rightarrow\mathrm{0}} {\sim}\:{y} \\ $$$$\underset{\begin{matrix}{{x}\rightarrow\mathrm{0}}\\{{x}\neq\mathrm{0}}\end{matrix}} {\mathrm{lim}}\:\frac{\mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{sin}^{\mathrm{2}} \left({x}\right)}\:=\:\underset{\begin{matrix}{{x}\rightarrow\mathrm{0}}\\{{x}\neq\mathrm{0}}\end{matrix}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:=\:\underset{\begin{matrix}{{x}\rightarrow\mathrm{0}}\\{{x}\neq\mathrm{0}}\end{matrix}} {\mathrm{lim}}\:\mathrm{1}\:=\:\mathrm{1} \\ $$
