Question Number 6908 by Tawakalitu. last updated on 02/Aug/16

$${sin}\left({Z}\right)\:=\:\mathrm{100} \\ $$$$ \\ $$$${find}\:{z}\: \\ $$
Commented by Rasheed Soomro last updated on 02/Aug/16
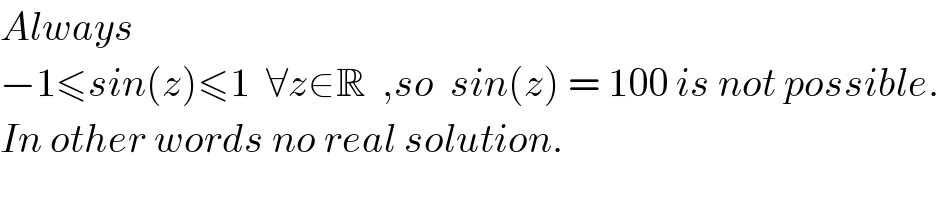
$${Always} \\ $$$$−\mathrm{1}\leqslant{sin}\left({z}\right)\leqslant\mathrm{1}\:\:\forall{z}\in\mathbb{R}\:\:,{so}\:\:{sin}\left({z}\right)\:=\:\mathrm{100}\:{is}\:{not}\:{possible}. \\ $$$${In}\:{other}\:{words}\:{no}\:{real}\:{solution}. \\ $$
Answered by sandy_suhendra last updated on 02/Aug/16
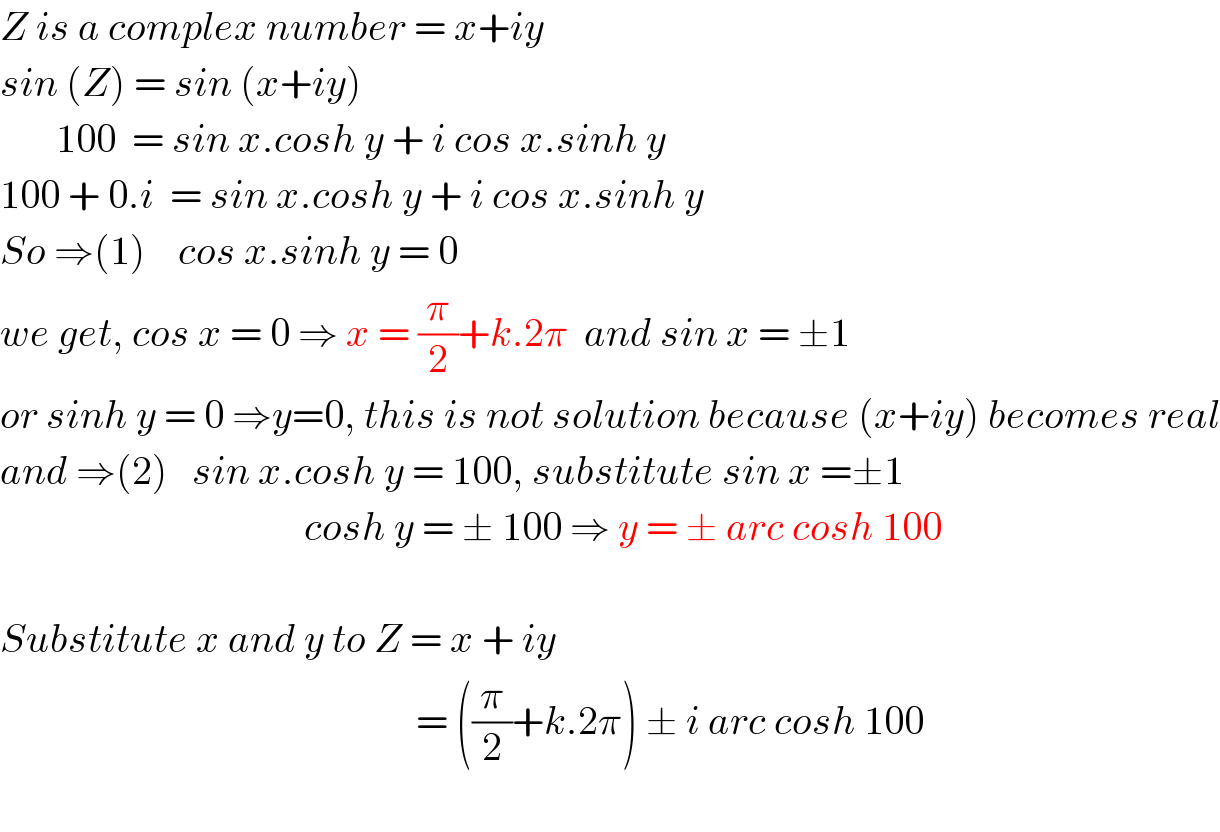
$${Z}\:{is}\:{a}\:{complex}\:{number}\:=\:{x}+{iy} \\ $$$${sin}\:\left({Z}\right)\:=\:{sin}\:\left({x}+{iy}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{100}\:\:=\:{sin}\:{x}.{cosh}\:{y}\:+\:{i}\:{cos}\:{x}.{sinh}\:{y} \\ $$$$\mathrm{100}\:+\:\mathrm{0}.{i}\:\:=\:{sin}\:{x}.{cosh}\:{y}\:+\:{i}\:{cos}\:{x}.{sinh}\:{y} \\ $$$${So}\:\Rightarrow\left(\mathrm{1}\right)\:\:\:\:{cos}\:{x}.{sinh}\:{y}\:=\:\mathrm{0} \\ $$$${we}\:{get},\:{cos}\:{x}\:=\:\mathrm{0}\:\Rightarrow\:{x}\:=\:\frac{\pi}{\mathrm{2}}+{k}.\mathrm{2}\pi\:\:{and}\:{sin}\:{x}\:=\:\pm\mathrm{1} \\ $$$${or}\:{sinh}\:{y}\:=\:\mathrm{0}\:\Rightarrow{y}=\mathrm{0},\:{this}\:{is}\:{not}\:{solution}\:{because}\:\left({x}+{iy}\right)\:{becomes}\:{real} \\ $$$${and}\:\Rightarrow\left(\mathrm{2}\right)\:\:\:{sin}\:{x}.{cosh}\:{y}\:=\:\mathrm{100},\:{substitute}\:{sin}\:{x}\:=\pm\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{cosh}\:{y}\:=\:\pm\:\mathrm{100}\:\Rightarrow\:{y}\:=\:\pm\:{arc}\:{cosh}\:\mathrm{100} \\ $$$$ \\ $$$${Substitute}\:{x}\:{and}\:{y}\:{to}\:{Z}\:=\:{x}\:+\:{iy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\frac{\pi}{\mathrm{2}}+{k}.\mathrm{2}\pi\right)\:\pm\:{i}\:{arc}\:{cosh}\:\mathrm{100} \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 02/Aug/16

$${Wow}\:…\:{Thanks}\:{for}\:{your}\:{help} \\ $$
Commented by Yozzii last updated on 03/Aug/16
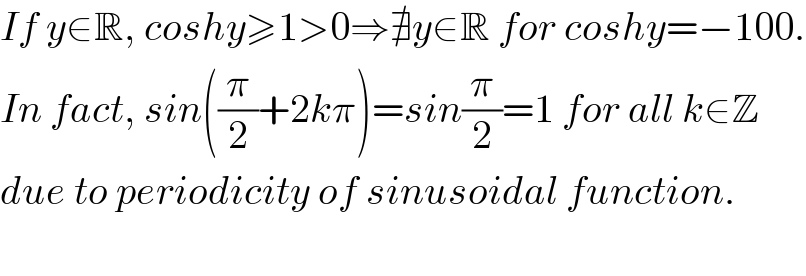
$${If}\:{y}\in\mathbb{R},\:{coshy}\geqslant\mathrm{1}>\mathrm{0}\Rightarrow\nexists{y}\in\mathbb{R}\:{for}\:{coshy}=−\mathrm{100}. \\ $$$${In}\:{fact},\:{sin}\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\right)={sin}\frac{\pi}{\mathrm{2}}=\mathrm{1}\:{for}\:{all}\:{k}\in\mathbb{Z} \\ $$$${due}\:{to}\:{periodicity}\:{of}\:{sinusoidal}\:{function}. \\ $$$$ \\ $$
