Question Number 206808 by mustafazaheen last updated on 26/Apr/24

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{10}^{\mathrm{x}} −\mathrm{1}}{\mathrm{x}^{\mathrm{10}} } \\ $$
Answered by mr W last updated on 26/Apr/24
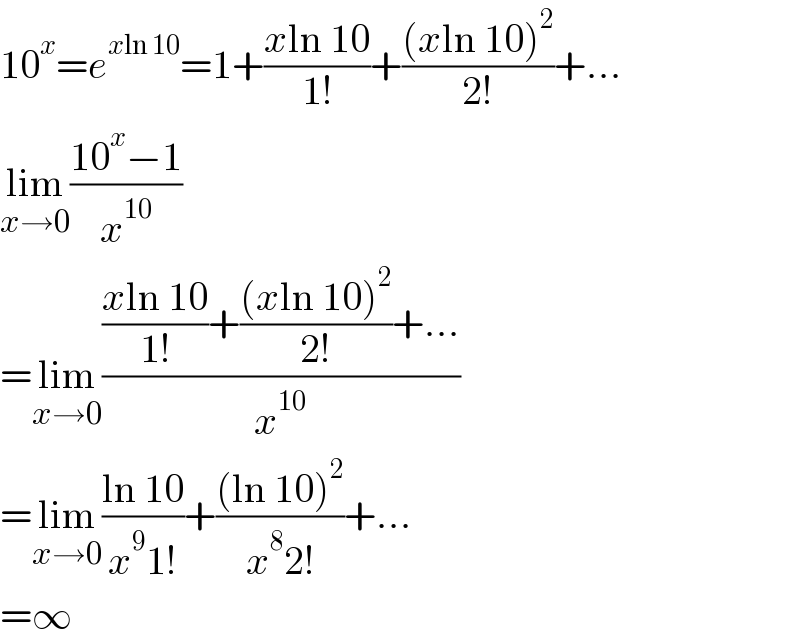
$$\mathrm{10}^{{x}} ={e}^{{x}\mathrm{ln}\:\mathrm{10}} =\mathrm{1}+\frac{{x}\mathrm{ln}\:\mathrm{10}}{\mathrm{1}!}+\frac{\left({x}\mathrm{ln}\:\mathrm{10}\right)^{\mathrm{2}} }{\mathrm{2}!}+… \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{10}^{{x}} −\mathrm{1}}{{x}^{\mathrm{10}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{x}\mathrm{ln}\:\mathrm{10}}{\mathrm{1}!}+\frac{\left({x}\mathrm{ln}\:\mathrm{10}\right)^{\mathrm{2}} }{\mathrm{2}!}+…}{{x}^{\mathrm{10}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\:\mathrm{10}}{{x}^{\mathrm{9}} \mathrm{1}!}+\frac{\left(\mathrm{ln}\:\mathrm{10}\right)^{\mathrm{2}} }{{x}^{\mathrm{8}} \mathrm{2}!}+… \\ $$$$=\infty \\ $$
Answered by lepuissantcedricjunior last updated on 26/Apr/24
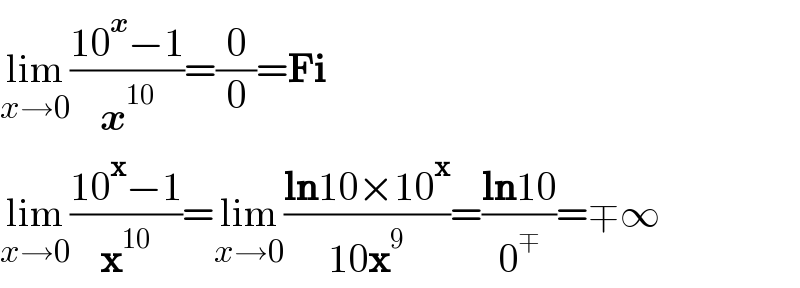
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{10}^{\boldsymbol{{x}}} −\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{10}} }=\frac{\mathrm{0}}{\mathrm{0}}=\boldsymbol{\mathrm{Fi}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{10}^{\boldsymbol{\mathrm{x}}} −\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{10}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{ln}}\mathrm{10}×\mathrm{10}^{\boldsymbol{\mathrm{x}}} }{\mathrm{10}\boldsymbol{\mathrm{x}}^{\mathrm{9}} }=\frac{\boldsymbol{\mathrm{ln}}\mathrm{10}}{\mathrm{0}^{\mp} }=\mp\infty \\ $$
