Question-72666

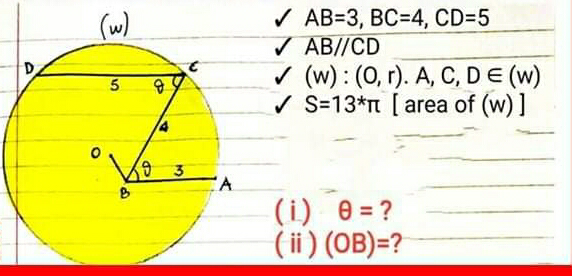
Question Number 72666 by aliesam last updated on 31/Oct/19

Answered by mind is power last updated on 31/Oct/19

let α=∠CDA=BAE ,OCA=2α E=(AD)∩BC (3/5)=((BE)/(EC)),BE+EC=4 ⇒BE=(3/2) AE^2 =(9/4)+9−2.(3/2).3cos(θ)=((45)/4)−9cos(θ)⇒AE=(3/2)(√(5−4cos(θ))) AC^2 =9+16−2.3.4cos(θ)=25−24cos(θ) ((AE)/(sin(θ)))=((BE)/(sin(α)))⇒sin(α)=((BE)/(AE)).sin(θ)=((sin(θ))/( (√(5−4cos(θ))))) AC^2 =oA^2 +OC^2 −2OA.OCcos(2α)=2R^2 (1−cos(2α))=52sin^2 (α) ⇔ { ((52sin^2 (α)=25−24cos(θ))),((sin(α)=((sin(θ))/( (√(5−4cos(θ))))))) :} ⇒((52sin^2 (θ))/(5−4cos(θ)))=25−24cos(θ) ⇒52(1−cos^2 (θ))=125+96cos^2 (θ)−220cos(θ) ⇔148cos^2 (θ)−220cos(θ)+73=0 Δ=220^2 −4.73.148=5184 cos(θ)=((220−72)/(296))=((148)/(296))=(1/2) cos(θ)=((292)/(296))=((73)/(74))....impossibl cos(DOC)=((2.13−5^2 )/(26))=(1/(26))⇒DOC≤90⇒DCO≥45 ⇒cos(θ)=cos(DcO)≤((√2)/2)⇒cos(θ)=(1/2)⇒θ=(π/3)=60^° BO DOC=cos^(−1) ((1/(26))) OCD=((π−DOC)/2) OCB=θ−OCD OC=(√(13)),CB=4 OB=(√(OC^2 +CB^2 −2OC.CBcos(OCB)))

$$\mathrm{let}\:\alpha=\angle\mathrm{CDA}=\mathrm{BAE}\:\:,\mathrm{OCA}=\mathrm{2}\alpha \\ $$$$\mathrm{E}=\left(\mathrm{AD}\right)\cap\mathrm{BC} \\ $$$$\frac{\mathrm{3}}{\mathrm{5}}=\frac{\mathrm{BE}}{\mathrm{EC}},\mathrm{BE}+\mathrm{EC}=\mathrm{4} \\ $$$$\Rightarrow\mathrm{BE}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{AE}^{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{4}}+\mathrm{9}−\mathrm{2}.\frac{\mathrm{3}}{\mathrm{2}}.\mathrm{3cos}\left(\theta\right)=\frac{\mathrm{45}}{\mathrm{4}}−\mathrm{9cos}\left(\theta\right)\Rightarrow\mathrm{AE}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{5}−\mathrm{4cos}\left(\theta\right)} \\ $$$$\mathrm{AC}^{\mathrm{2}} =\mathrm{9}+\mathrm{16}−\mathrm{2}.\mathrm{3}.\mathrm{4cos}\left(\theta\right)=\mathrm{25}−\mathrm{24cos}\left(\theta\right) \\ $$$$\frac{\mathrm{AE}}{\mathrm{sin}\left(\theta\right)}=\frac{\mathrm{BE}}{\mathrm{sin}\left(\alpha\right)}\Rightarrow\mathrm{sin}\left(\alpha\right)=\frac{\mathrm{BE}}{\mathrm{AE}}.\mathrm{sin}\left(\theta\right)=\frac{\mathrm{sin}\left(\theta\right)}{\:\sqrt{\mathrm{5}−\mathrm{4cos}\left(\theta\right)}} \\ $$$$\mathrm{AC}^{\mathrm{2}} =\mathrm{oA}^{\mathrm{2}} +\mathrm{OC}^{\mathrm{2}} −\mathrm{2OA}.\mathrm{OCcos}\left(\mathrm{2}\alpha\right)=\mathrm{2R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2}\alpha\right)\right)=\mathrm{52sin}^{\mathrm{2}} \left(\alpha\right) \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{52sin}^{\mathrm{2}} \left(\alpha\right)=\mathrm{25}−\mathrm{24cos}\left(\theta\right)}\\{\mathrm{sin}\left(\alpha\right)=\frac{\mathrm{sin}\left(\theta\right)}{\:\sqrt{\mathrm{5}−\mathrm{4cos}\left(\theta\right)}}}\end{cases} \\ $$$$\Rightarrow\frac{\mathrm{52sin}^{\mathrm{2}} \left(\theta\right)}{\mathrm{5}−\mathrm{4cos}\left(\theta\right)}=\mathrm{25}−\mathrm{24cos}\left(\theta\right) \\ $$$$\Rightarrow\mathrm{52}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \left(\theta\right)\right)=\mathrm{125}+\mathrm{96cos}^{\mathrm{2}} \left(\theta\right)−\mathrm{220cos}\left(\theta\right) \\ $$$$\Leftrightarrow\mathrm{148cos}^{\mathrm{2}} \left(\theta\right)−\mathrm{220cos}\left(\theta\right)+\mathrm{73}=\mathrm{0} \\ $$$$\Delta=\mathrm{220}^{\mathrm{2}} −\mathrm{4}.\mathrm{73}.\mathrm{148}=\mathrm{5184} \\ $$$$\mathrm{cos}\left(\theta\right)=\frac{\mathrm{220}−\mathrm{72}}{\mathrm{296}}=\frac{\mathrm{148}}{\mathrm{296}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\left(\theta\right)=\frac{\mathrm{292}}{\mathrm{296}}=\frac{\mathrm{73}}{\mathrm{74}}….\mathrm{impossibl} \\ $$$$\mathrm{cos}\left(\mathrm{DOC}\right)=\frac{\mathrm{2}.\mathrm{13}−\mathrm{5}^{\mathrm{2}} }{\mathrm{26}}=\frac{\mathrm{1}}{\mathrm{26}}\Rightarrow\mathrm{DOC}\leqslant\mathrm{90}\Rightarrow\mathrm{DCO}\geqslant\mathrm{45} \\ $$$$\Rightarrow\mathrm{cos}\left(\theta\right)=\mathrm{cos}\left(\mathrm{DcO}\right)\leqslant\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\Rightarrow\mathrm{cos}\left(\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\theta=\frac{\pi}{\mathrm{3}}=\mathrm{60}^{°} \\ $$$$\mathrm{BO} \\ $$$$\mathrm{DOC}=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{26}}\right) \\ $$$$\mathrm{OCD}=\frac{\pi−\mathrm{DOC}}{\mathrm{2}} \\ $$$$\mathrm{OCB}=\theta−\mathrm{OCD} \\ $$$$\mathrm{OC}=\sqrt{\mathrm{13}},\mathrm{CB}=\mathrm{4} \\ $$$$\mathrm{OB}=\sqrt{\mathrm{OC}^{\mathrm{2}} +\mathrm{CB}^{\mathrm{2}} −\mathrm{2OC}.\mathrm{CBcos}\left(\mathrm{OCB}\right)} \\ $$

Commented by aliesam last updated on 31/Oct/19

$${nice}\:{solution}\:{sir}\:{god}\:{bless}\:{you} \\ $$

Commented by mind is power last updated on 01/Nov/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply