Question Number 66101 by Rio Michael last updated on 09/Aug/19
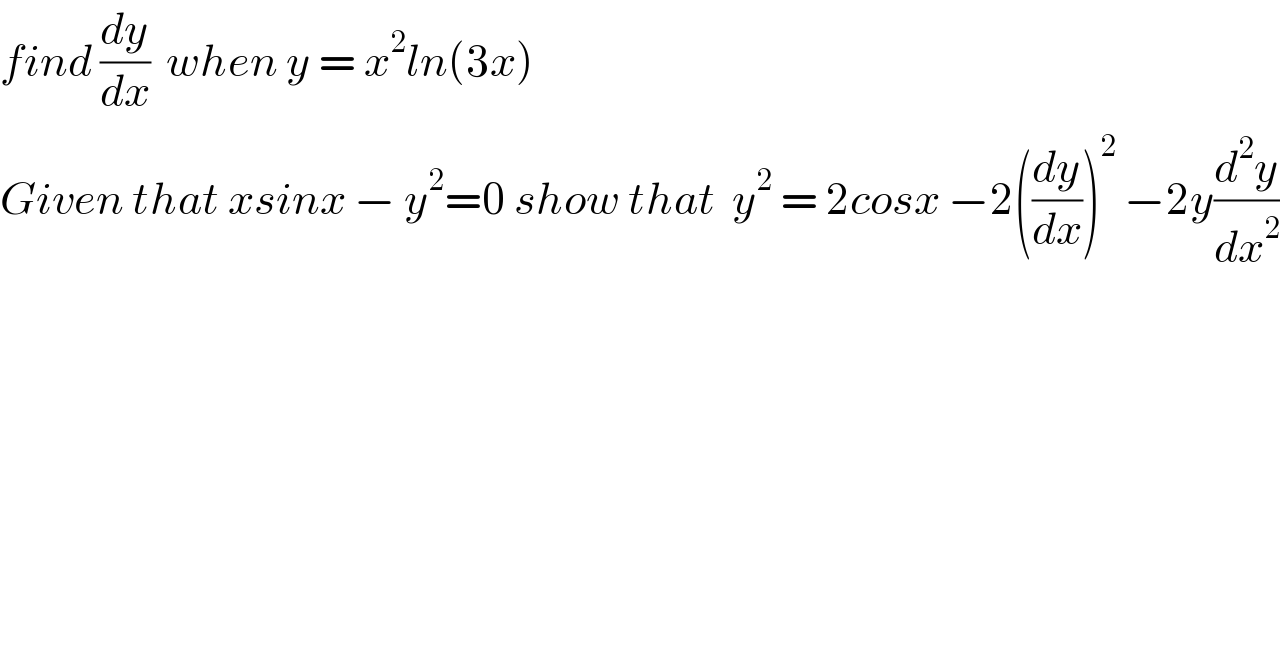
$${find}\:\frac{{dy}}{{dx}}\:\:{when}\:{y}\:=\:{x}^{\mathrm{2}} {ln}\left(\mathrm{3}{x}\right) \\ $$$${Given}\:{that}\:{xsinx}\:−\:{y}^{\mathrm{2}} =\mathrm{0}\:{show}\:{that}\:\:{y}^{\mathrm{2}} \:=\:\mathrm{2}{cosx}\:−\mathrm{2}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} \:−\mathrm{2}{y}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} } \\ $$
Commented by Prithwish sen last updated on 09/Aug/19
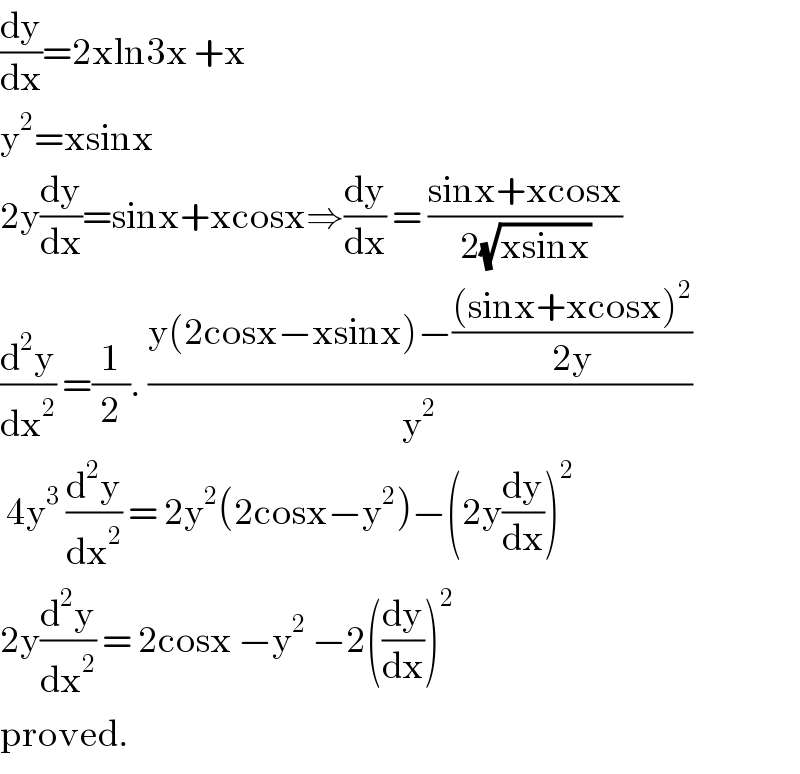
$$\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{2xln3x}\:+\mathrm{x} \\ $$$$\mathrm{y}^{\mathrm{2}} =\mathrm{xsinx} \\ $$$$\mathrm{2y}\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{sinx}+\mathrm{xcosx}\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{sinx}+\mathrm{xcosx}}{\mathrm{2}\sqrt{\mathrm{xsinx}}} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}.\:\frac{\mathrm{y}\left(\mathrm{2cosx}−\mathrm{xsinx}\right)−\frac{\left(\mathrm{sinx}+\mathrm{xcosx}\right)^{\mathrm{2}} }{\mathrm{2y}}}{\mathrm{y}^{\mathrm{2}} } \\ $$$$\:\mathrm{4y}^{\mathrm{3}} \:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:\mathrm{2y}^{\mathrm{2}} \left(\mathrm{2cosx}−\mathrm{y}^{\mathrm{2}} \right)−\left(\mathrm{2y}\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2y}\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:\mathrm{2cosx}\:−\mathrm{y}^{\mathrm{2}} \:−\mathrm{2}\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} \\ $$$$\mathrm{proved}. \\ $$
Answered by GordonYeeman last updated on 09/Aug/19
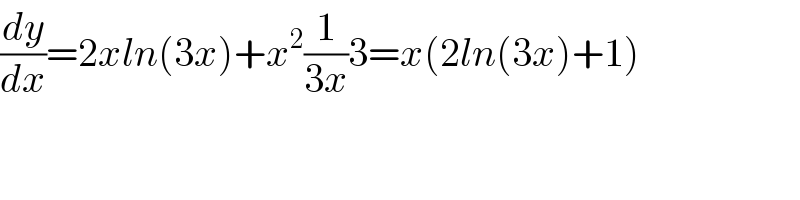
$$\frac{{dy}}{{dx}}=\mathrm{2}{xln}\left(\mathrm{3}{x}\right)+{x}^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{3}{x}}\mathrm{3}={x}\left(\mathrm{2}{ln}\left(\mathrm{3}{x}\right)+\mathrm{1}\right) \\ $$
