Question Number 66103 by Rio Michael last updated on 09/Aug/19

$${A}\:{binary}\:{relation}\:{R}\:{is}\:{defined}\:{on}\:\mathbb{N},{the}\:{set}\:{of}\:{natural}\:{numbers}\:{by}\: \\ $$$$\:_{{x}} {R}_{{y}} \:\Leftrightarrow\:\exists\:{n}\:\in\:\mathbb{Z}\::\:{x}\:=\:\mathrm{2}^{{n}} {y},\:\:{x},{y}\:\in\:\mathbb{N} \\ $$$${show}\:{that}\:{R}\:{is}\:{an}\:{equivalence}\:{relation} \\ $$
Commented by Prithwish sen last updated on 09/Aug/19
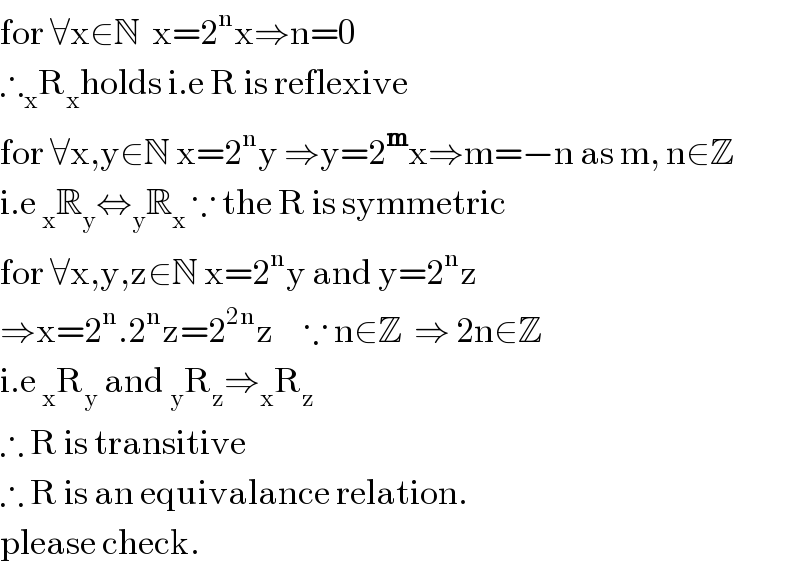
$$\mathrm{for}\:\forall\mathrm{x}\in\mathbb{N}\:\:\mathrm{x}=\mathrm{2}^{\mathrm{n}} \mathrm{x}\Rightarrow\mathrm{n}=\mathrm{0} \\ $$$$\therefore_{\mathrm{x}} \mathrm{R}_{\mathrm{x}} \mathrm{holds}\:\mathrm{i}.\mathrm{e}\:\mathrm{R}\:\mathrm{is}\:\mathrm{reflexive} \\ $$$$\mathrm{for}\:\forall\mathrm{x},\mathrm{y}\in\mathbb{N}\:\mathrm{x}=\mathrm{2}^{\mathrm{n}} \mathrm{y}\:\Rightarrow\mathrm{y}=\mathrm{2}^{\boldsymbol{\mathrm{m}}} \mathrm{x}\Rightarrow\mathrm{m}=−\mathrm{n}\:\mathrm{as}\:\mathrm{m},\:\mathrm{n}\in\mathbb{Z} \\ $$$$\mathrm{i}.\mathrm{e}\:_{\mathrm{x}} \mathbb{R}_{\mathrm{y}} \Leftrightarrow_{\mathrm{y}} \mathbb{R}_{\mathrm{x}} \:\because\:\mathrm{the}\:\mathrm{R}\:\mathrm{is}\:\mathrm{symmetric} \\ $$$$\mathrm{for}\:\forall\mathrm{x},\mathrm{y},\mathrm{z}\in\mathbb{N}\:\mathrm{x}=\mathrm{2}^{\mathrm{n}} \mathrm{y}\:\mathrm{and}\:\mathrm{y}=\mathrm{2}^{\mathrm{n}} \mathrm{z} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{2}^{\mathrm{n}} .\mathrm{2}^{\mathrm{n}} \mathrm{z}=\mathrm{2}^{\mathrm{2n}} \mathrm{z}\:\:\:\:\:\because\:\mathrm{n}\in\mathbb{Z}\:\:\Rightarrow\:\mathrm{2n}\in\mathbb{Z} \\ $$$$\mathrm{i}.\mathrm{e}\:_{\mathrm{x}} \mathrm{R}_{\mathrm{y}} \:\mathrm{and}\:_{\mathrm{y}} \mathrm{R}_{\mathrm{z}} \Rightarrow_{\mathrm{x}} \mathrm{R}_{\mathrm{z}} \\ $$$$\therefore\:\mathrm{R}\:\mathrm{is}\:\mathrm{transitive} \\ $$$$\therefore\:\mathrm{R}\:\mathrm{is}\:\mathrm{an}\:\mathrm{equivalance}\:\mathrm{relation}. \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$
Commented by Rio Michael last updated on 09/Aug/19

$${thank}\:{you}\:{sir} \\ $$
