Question Number 138249 by sahnaz last updated on 11/Apr/21

$$\mathrm{li}\underset{\mathrm{n}\rightarrow\mathrm{0}} {\mathrm{m}}\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}} +\mathrm{3}^{\mathrm{n}+\mathrm{2}} +\mathrm{4}^{\mathrm{n}+\mathrm{3}} }{\mathrm{2}^{\mathrm{n}} +\mathrm{3}^{\mathrm{n}} +\mathrm{4}^{\mathrm{n}} } \\ $$
Answered by mathmax by abdo last updated on 11/Apr/21
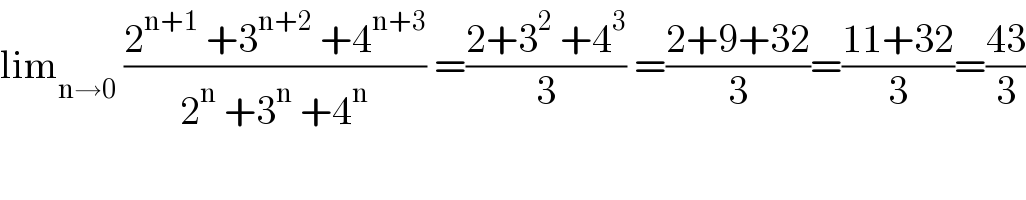
$$\mathrm{lim}_{\mathrm{n}\rightarrow\mathrm{0}} \:\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}} \:+\mathrm{3}^{\mathrm{n}+\mathrm{2}} \:+\mathrm{4}^{\mathrm{n}+\mathrm{3}} }{\mathrm{2}^{\mathrm{n}} \:+\mathrm{3}^{\mathrm{n}} \:+\mathrm{4}^{\mathrm{n}} }\:=\frac{\mathrm{2}+\mathrm{3}^{\mathrm{2}} \:+\mathrm{4}^{\mathrm{3}} }{\mathrm{3}}\:=\frac{\mathrm{2}+\mathrm{9}+\mathrm{32}}{\mathrm{3}}=\frac{\mathrm{11}+\mathrm{32}}{\mathrm{3}}=\frac{\mathrm{43}}{\mathrm{3}} \\ $$
