Question Number 7243 by Sh505146@gmail.com last updated on 18/Aug/16
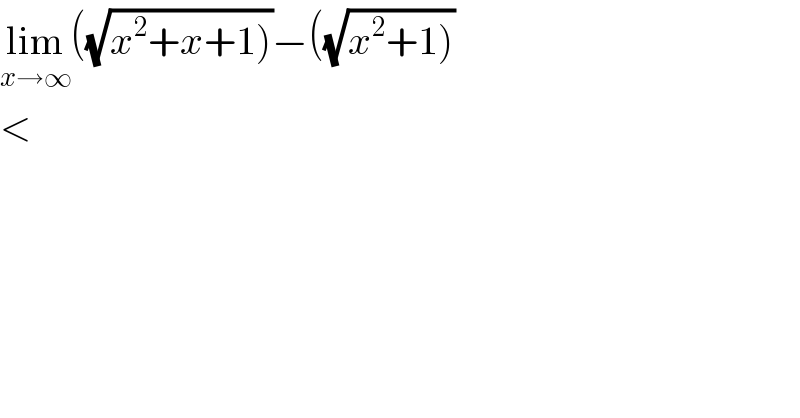
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt{\left.{x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}−\left(\sqrt{\left.{x}^{\mathrm{2}} +\mathrm{1}\right)}\right.\right. \\ $$$$< \\ $$
Commented by Rasheed Soomro last updated on 18/Aug/16
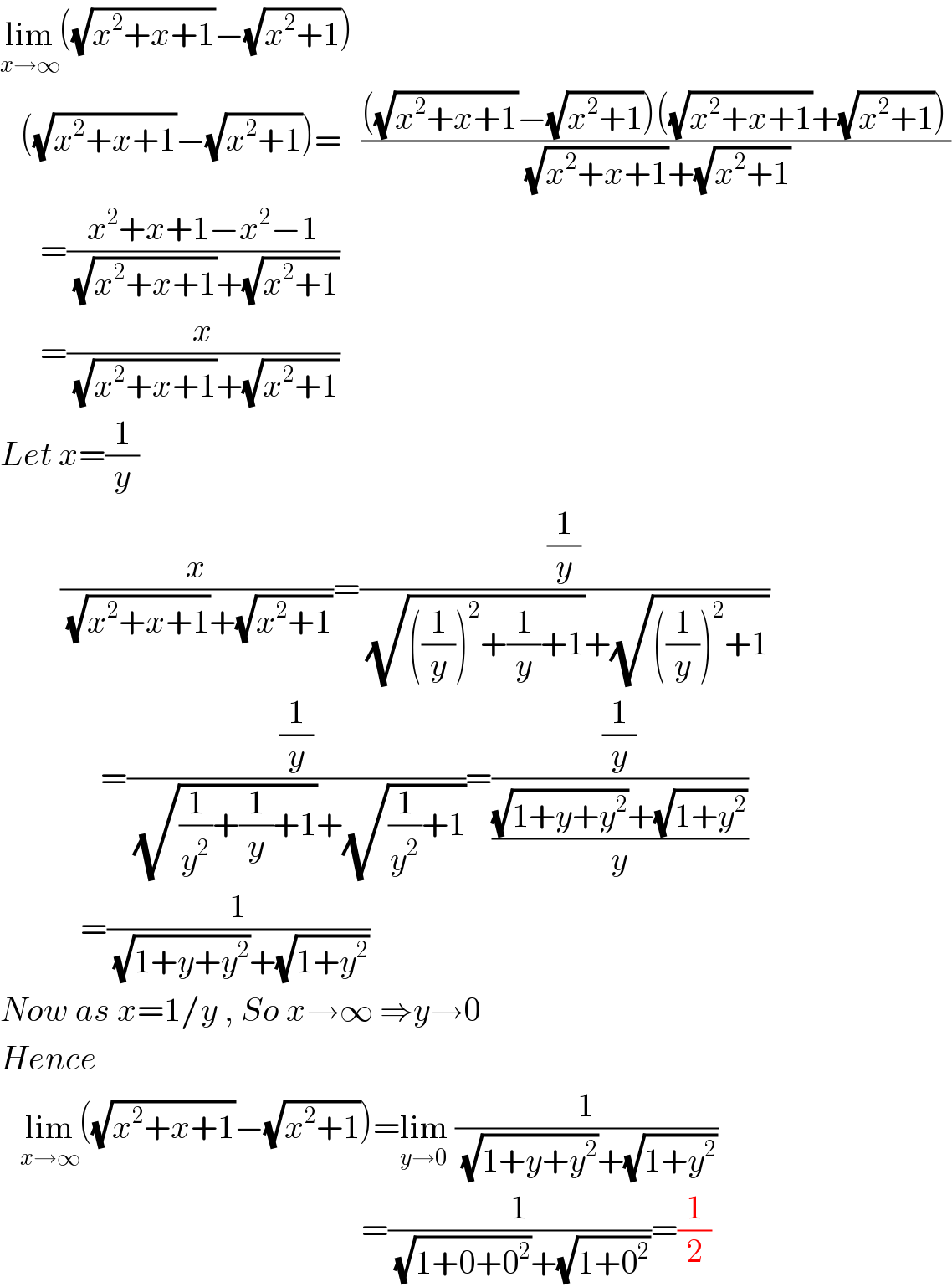
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$\:\:\:\left(\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)=\:\:\:\frac{\left(\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\left(\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\:\:\:\:\:\:=\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}−{x}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\:\:\:\:\:\:=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${Let}\:{x}=\frac{\mathrm{1}}{{y}} \\ $$$$\:\:\:\:\:\:\:\:\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}=\frac{\frac{\mathrm{1}}{{y}}}{\:\sqrt{\left(\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{{y}}+\mathrm{1}}+\sqrt{\left(\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\frac{\mathrm{1}}{{y}}}{\:\sqrt{\frac{\mathrm{1}}{{y}^{\mathrm{2}} }+\frac{\mathrm{1}}{{y}}+\mathrm{1}}+\sqrt{\frac{\mathrm{1}}{{y}^{\mathrm{2}} }+\mathrm{1}}}=\frac{\frac{\mathrm{1}}{{y}}}{\frac{\sqrt{\mathrm{1}+{y}+{y}^{\mathrm{2}} }+\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }}{{y}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{y}+{y}^{\mathrm{2}} }+\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }} \\ $$$${Now}\:{as}\:{x}=\mathrm{1}/{y}\:,\:{So}\:{x}\rightarrow\infty\:\Rightarrow{y}\rightarrow\mathrm{0} \\ $$$${Hence}\: \\ $$$$\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)=\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{y}+{y}^{\mathrm{2}} }+\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{0}+\mathrm{0}^{\mathrm{2}} }+\sqrt{\mathrm{1}+\mathrm{0}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by peter james last updated on 19/Aug/16

$${welldone}.. \\ $$
