Question Number 66107 by Rio Michael last updated on 09/Aug/19
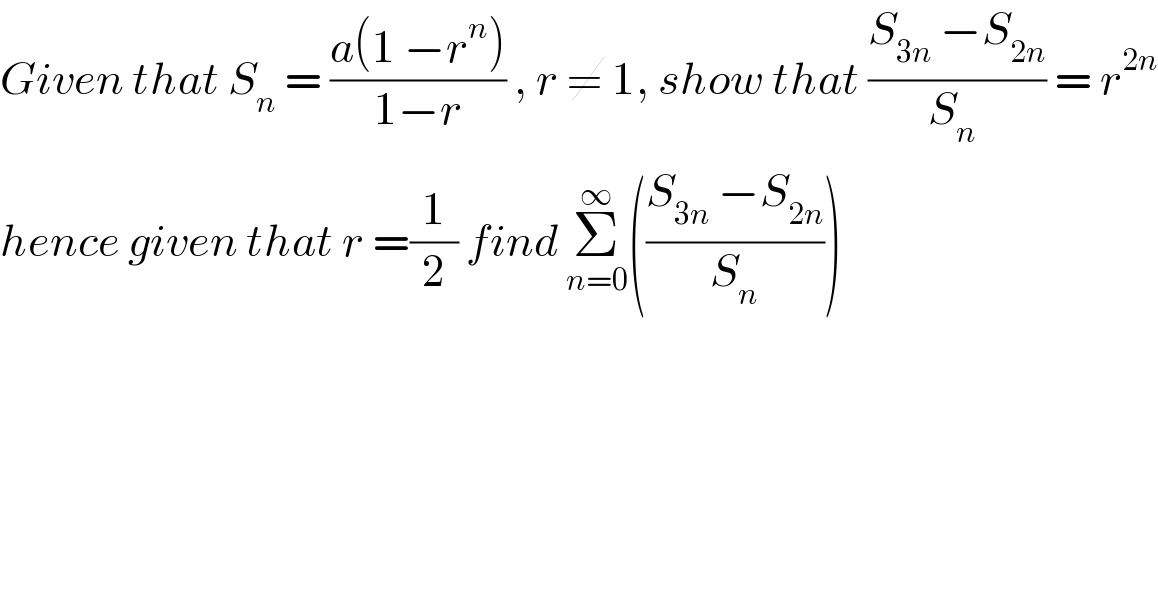
$${Given}\:{that}\:{S}_{{n}} \:=\:\frac{{a}\left(\mathrm{1}\:−{r}^{{n}} \right)}{\mathrm{1}−{r}}\:,\:{r}\:\neq\:\mathrm{1},\:{show}\:{that}\:\frac{{S}_{\mathrm{3}{n}} \:−{S}_{\mathrm{2}{n}} }{{S}_{{n}} \:}\:=\:{r}^{\mathrm{2}{n}} \\ $$$${hence}\:{given}\:{that}\:{r}\:=\frac{\mathrm{1}}{\mathrm{2}}\:{find}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{{S}_{\mathrm{3}{n}} \:−{S}_{\mathrm{2}{n}} }{{S}_{{n}} }\right) \\ $$
Commented by Prithwish sen last updated on 09/Aug/19
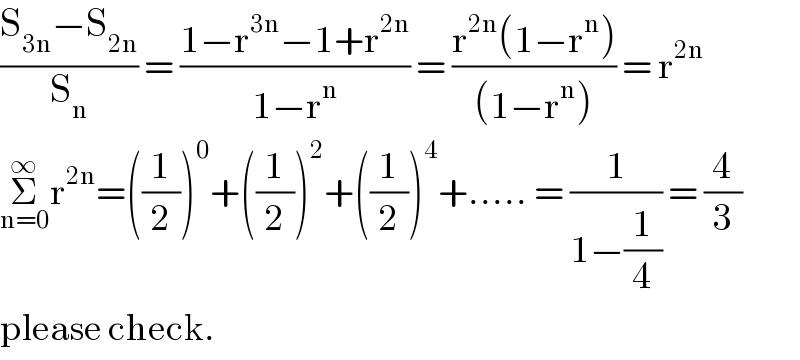
$$\frac{\mathrm{S}_{\mathrm{3n}} −\mathrm{S}_{\mathrm{2n}} }{\mathrm{S}_{\mathrm{n}} }\:=\:\frac{\mathrm{1}−\mathrm{r}^{\mathrm{3n}} −\mathrm{1}+\mathrm{r}^{\mathrm{2n}} }{\mathrm{1}−\mathrm{r}^{\mathrm{n}} }\:=\:\frac{\mathrm{r}^{\mathrm{2n}} \left(\mathrm{1}−\mathrm{r}^{\mathrm{n}} \right)}{\left(\mathrm{1}−\mathrm{r}^{\mathrm{n}} \right)}\:=\:\mathrm{r}^{\mathrm{2n}} \\ $$$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{r}^{\mathrm{2n}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{0}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{4}} +…..\:=\:\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$
Commented by Rio Michael last updated on 09/Aug/19
$${correct}\:{sir}\:{thanks} \\ $$
Commented by mathmax by abdo last updated on 10/Aug/19
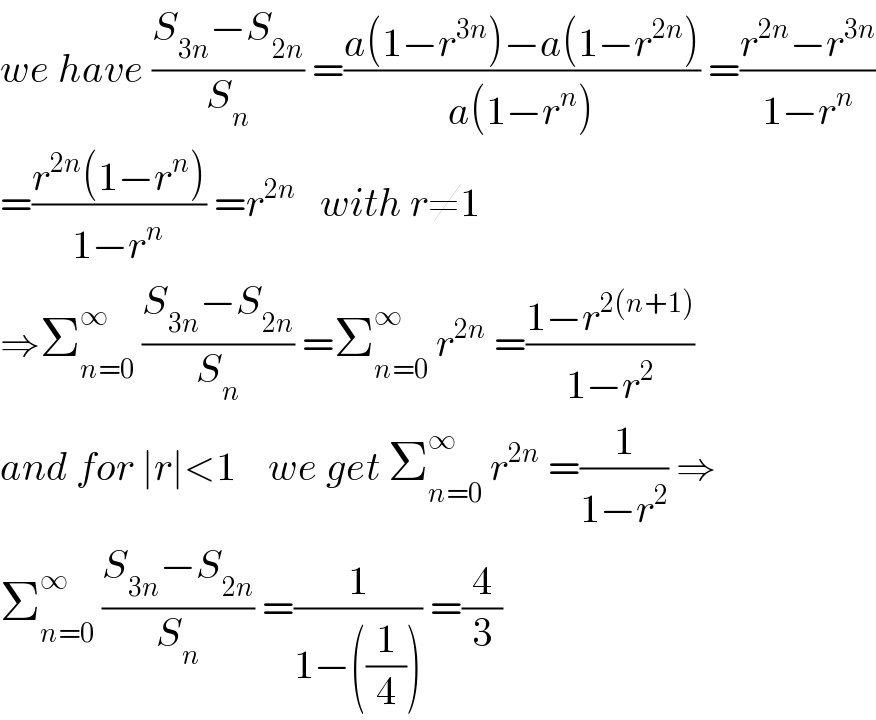
$${we}\:{have}\:\frac{{S}_{\mathrm{3}{n}} −{S}_{\mathrm{2}{n}} }{{S}_{{n}} }\:=\frac{{a}\left(\mathrm{1}−{r}^{\mathrm{3}{n}} \right)−{a}\left(\mathrm{1}−{r}^{\mathrm{2}{n}} \right)}{{a}\left(\mathrm{1}−{r}^{{n}} \right)}\:=\frac{{r}^{\mathrm{2}{n}} −{r}^{\mathrm{3}{n}} }{\mathrm{1}−{r}^{{n}} } \\ $$$$=\frac{{r}^{\mathrm{2}{n}} \left(\mathrm{1}−{r}^{{n}} \right)}{\mathrm{1}−{r}^{{n}} }\:={r}^{\mathrm{2}{n}} \:\:\:{with}\:{r}\neq\mathrm{1} \\ $$$$\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{S}_{\mathrm{3}{n}} −{S}_{\mathrm{2}{n}} }{{S}_{{n}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:{r}^{\mathrm{2}{n}} \:=\frac{\mathrm{1}−{r}^{\mathrm{2}\left({n}+\mathrm{1}\right)} }{\mathrm{1}−{r}^{\mathrm{2}} } \\ $$$${and}\:{for}\:\mid{r}\mid<\mathrm{1}\:\:\:\:{we}\:{get}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{r}^{\mathrm{2}{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−{r}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{S}_{\mathrm{3}{n}} −{S}_{\mathrm{2}{n}} }{{S}_{{n}} }\:=\frac{\mathrm{1}}{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}\:=\frac{\mathrm{4}}{\mathrm{3}} \\ $$
