Question Number 7314 by Rasheed Soomro last updated on 23/Aug/16
Commented by Rasheed Soomro last updated on 23/Aug/16

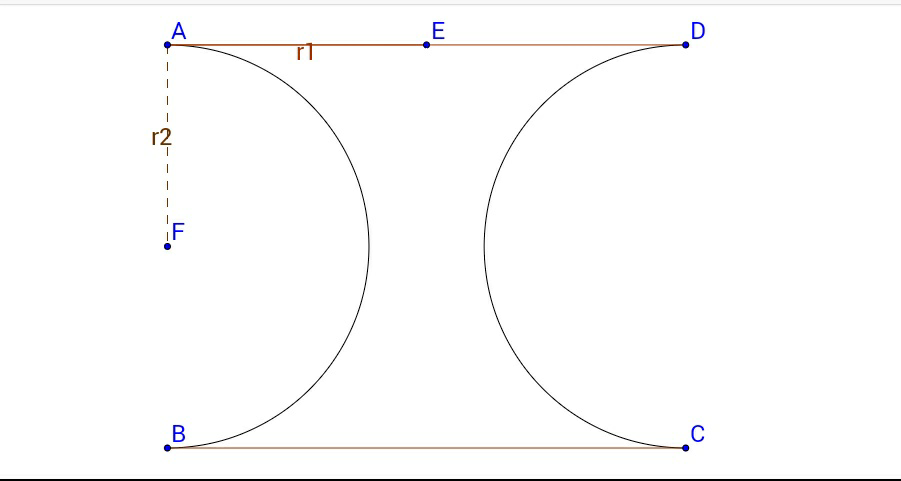
$${Top}\:{and}\:{bottom}\:{of}\:{a}\:{solid}\:{are}\:{congruent}\:{circles}. \\ $$$${Above}\:{is}\:{the}\:{cross}-{section}\:{of}\:{the}\:{solid},\:{which}\: \\ $$$${is}\:{obtained}\:{by}\:{cutting}\:{the}\:{solid}\:{in}\:{two}\:{equal}\:{parts}. \\ $$$${Find}\:{out}\:{the}\:{volume}\:{of}\:{the}\:{solid}. \\ $$
Answered by Yozzia last updated on 24/Aug/16
![Define the circle w with cartesian equation x^2 +(y−r_1 )^2 =r_2 ^2 where r_1 >r_2 >0. ⇒y=r_1 ±(√(r_2 ^2 −x^2 )) {∣x∣≤r_2 }. The problem given can be viewed as finding the volume V of the figure generated when a part of w, whose y coordinates satisfy 0<y≤r_1 , is rotated 2π radians about the x−axis. ∴ y=r_1 −(√(r_2 ^2 −x^2 )) {∣x∣≤r_2 }. Using V=π∫_(−r_2 ) ^( r_2 ) y^2 dx we get V=2π∫_0 ^r_2 (r_1 −(√(r_2 ^2 −x^2 )))^2 dx {y^2 is even}. V=2π∫_0 ^r_2 {r_1 ^2 +r_2 ^2 −x^2 −2r_1 (√(r_2 ^2 −x^2 ))}dx Let x=r_2 sinθ 0≤θ≤2π.⇒dx=r_2 cosθdθ. At x=0,θ=0 and at x=r_2 , θ=(π/2). ∴V=2πr_2 ∫_0 ^(π/2) {r_1 ^2 +r_2 ^2 −r_2 ^2 sin^2 θ−2r_1 (√(r_2 ^2 −r_2 ^2 sin^2 θ))}cosθdθ V=2πr_2 [∫_0 ^(π/2) (r_1 ^2 +r_2 ^2 )cosθ dθ−r_2 ^2 ∫_0 ^(π/2) sin^2 θcosθdθ−2r_1 r_2 ∫_0 ^(π/2) cos^2 θdθ] V=2πr_2 [r_1 ^2 +r_2 ^2 −{((r_2 ^2 u^3 )/3)}_0 ^1 −r_1 r_2 ∫_0 ^(π/2) (1+cos2θ)dθ] V=2πr_2 [r_1 ^2 +r_2 ^2 −(r_2 ^2 /3)−r_1 r_2 {θ+(1/2)sin2θ}_0 ^(π/2) ] V=2πr_2 [r_1 ^2 +(2/3)r_2 ^2 −((r_1 r_2 π)/2)] V=((πr_2 )/3)[6r_1 ^2 +4r_2 ^2 −3πr_1 r_2 ] V=((2πr_2 )/3)(3r_1 ^2 +2r_2 ^2 )−π^2 r_1 r_2 ^2 V=2πr_1 ^2 r_2 +((4πr_2 ^3 )/3)−π^2 r_2 ^2 r_1 −−−−−−−−−−−−−−−−−−−−−−−−−− By Pappus−Guldin theorem, V=2πAy^� where A=area bounded between y=r_1 −(√(r_2 ^2 −x^2 )), lines y=0, x=±r_2 and y^� =distance of centroid of A from axis of rotation (y=0). ∴ y^� =(V/(2πA)). It can be shown that A=((r_2 (4r_1 −πr_2 ))/2). ∴ y^� =((((πr_2 )/3)(6r_1 ^2 +4r_2 ^2 −3πr_1 r_2 ))/(2π((r_2 (4r_1 −πr_2 ))/2))) or y^� =((6r_1 ^2 +4r_2 ^2 −3πr_1 r_2 )/(3(4r_1 −πr_2 )))](https://www.tinkutara.com/question/Q7336.png)
$${Define}\:{the}\:{circle}\:{w}\:{with}\:{cartesian} \\ $$$${equation}\:{x}^{\mathrm{2}} +\left({y}−{r}_{\mathrm{1}} \right)^{\mathrm{2}} ={r}_{\mathrm{2}} ^{\mathrm{2}} \:{where}\:{r}_{\mathrm{1}} >{r}_{\mathrm{2}} >\mathrm{0}. \\ $$$$\Rightarrow{y}={r}_{\mathrm{1}} \pm\sqrt{{r}_{\mathrm{2}} ^{\mathrm{2}} −{x}^{\mathrm{2}} }\:\:\left\{\mid{x}\mid\leqslant{r}_{\mathrm{2}} \right\}. \\ $$$${The}\:{problem}\:{given}\:{can}\:{be}\:{viewed}\:{as}\:{finding} \\ $$$${the}\:{volume}\:{V}\:{of}\:{the}\:{figure}\:{generated} \\ $$$${when}\:{a}\:{part}\:{of}\:{w},\:{whose}\:{y}\:{coordinates} \\ $$$${satisfy}\:\mathrm{0}<{y}\leqslant{r}_{\mathrm{1}} ,\:{is}\:{rotated}\:\mathrm{2}\pi\:{radians} \\ $$$${about}\:{the}\:{x}−{axis}. \\ $$$$\therefore\:{y}={r}_{\mathrm{1}} −\sqrt{{r}_{\mathrm{2}} ^{\mathrm{2}} −{x}^{\mathrm{2}} }\:\:\:\:\left\{\mid{x}\mid\leqslant{r}_{\mathrm{2}} \right\}. \\ $$$${Using}\:{V}=\pi\int_{−{r}_{\mathrm{2}} } ^{\:{r}_{\mathrm{2}} } {y}^{\mathrm{2}} {dx}\:{we}\:{get} \\ $$$${V}=\mathrm{2}\pi\int_{\mathrm{0}} ^{{r}_{\mathrm{2}} } \left({r}_{\mathrm{1}} −\sqrt{{r}_{\mathrm{2}} ^{\mathrm{2}} −{x}^{\mathrm{2}} }\right)^{\mathrm{2}} {dx}\:\:\:\left\{{y}^{\mathrm{2}} \:{is}\:{even}\right\}. \\ $$$${V}=\mathrm{2}\pi\int_{\mathrm{0}} ^{{r}_{\mathrm{2}} } \left\{{r}_{\mathrm{1}} ^{\mathrm{2}} +{r}_{\mathrm{2}} ^{\mathrm{2}} −{x}^{\mathrm{2}} −\mathrm{2}{r}_{\mathrm{1}} \sqrt{{r}_{\mathrm{2}} ^{\mathrm{2}} −{x}^{\mathrm{2}} }\right\}{dx} \\ $$$${Let}\:{x}={r}_{\mathrm{2}} {sin}\theta\:\:\mathrm{0}\leqslant\theta\leqslant\mathrm{2}\pi.\Rightarrow{dx}={r}_{\mathrm{2}} {cos}\theta{d}\theta. \\ $$$${At}\:{x}=\mathrm{0},\theta=\mathrm{0}\:{and}\:{at}\:{x}={r}_{\mathrm{2}} ,\:\theta=\frac{\pi}{\mathrm{2}}. \\ $$$$\therefore{V}=\mathrm{2}\pi{r}_{\mathrm{2}} \int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left\{{r}_{\mathrm{1}} ^{\mathrm{2}} +{r}_{\mathrm{2}} ^{\mathrm{2}} −{r}_{\mathrm{2}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta−\mathrm{2}{r}_{\mathrm{1}} \sqrt{{r}_{\mathrm{2}} ^{\mathrm{2}} −{r}_{\mathrm{2}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\right\}{cos}\theta{d}\theta \\ $$$${V}=\mathrm{2}\pi{r}_{\mathrm{2}} \left[\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left({r}_{\mathrm{1}} ^{\mathrm{2}} +{r}_{\mathrm{2}} ^{\mathrm{2}} \right){cos}\theta\:{d}\theta−{r}_{\mathrm{2}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\pi/\mathrm{2}} {sin}^{\mathrm{2}} \theta{cos}\theta{d}\theta−\mathrm{2}{r}_{\mathrm{1}} {r}_{\mathrm{2}} \int_{\mathrm{0}} ^{\pi/\mathrm{2}} {cos}^{\mathrm{2}} \theta{d}\theta\right] \\ $$$${V}=\mathrm{2}\pi{r}_{\mathrm{2}} \left[{r}_{\mathrm{1}} ^{\mathrm{2}} +{r}_{\mathrm{2}} ^{\mathrm{2}} −\left\{\frac{{r}_{\mathrm{2}} ^{\mathrm{2}} {u}^{\mathrm{3}} }{\mathrm{3}}\right\}_{\mathrm{0}} ^{\mathrm{1}} −{r}_{\mathrm{1}} {r}_{\mathrm{2}} \int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{1}+{cos}\mathrm{2}\theta\right){d}\theta\right] \\ $$$${V}=\mathrm{2}\pi{r}_{\mathrm{2}} \left[{r}_{\mathrm{1}} ^{\mathrm{2}} +{r}_{\mathrm{2}} ^{\mathrm{2}} −\frac{{r}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{3}}−{r}_{\mathrm{1}} {r}_{\mathrm{2}} \left\{\theta+\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}\theta\right\}_{\mathrm{0}} ^{\pi/\mathrm{2}} \right] \\ $$$${V}=\mathrm{2}\pi{r}_{\mathrm{2}} \left[{r}_{\mathrm{1}} ^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{3}}{r}_{\mathrm{2}} ^{\mathrm{2}} −\frac{{r}_{\mathrm{1}} {r}_{\mathrm{2}} \pi}{\mathrm{2}}\right] \\ $$$${V}=\frac{\pi{r}_{\mathrm{2}} }{\mathrm{3}}\left[\mathrm{6}{r}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{4}{r}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{3}\pi{r}_{\mathrm{1}} {r}_{\mathrm{2}} \right] \\ $$$${V}=\frac{\mathrm{2}\pi{r}_{\mathrm{2}} }{\mathrm{3}}\left(\mathrm{3}{r}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{2}{r}_{\mathrm{2}} ^{\mathrm{2}} \right)−\pi^{\mathrm{2}} {r}_{\mathrm{1}} {r}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${V}=\mathrm{2}\pi{r}_{\mathrm{1}} ^{\mathrm{2}} {r}_{\mathrm{2}} +\frac{\mathrm{4}\pi{r}_{\mathrm{2}} ^{\mathrm{3}} }{\mathrm{3}}−\pi^{\mathrm{2}} {r}_{\mathrm{2}} ^{\mathrm{2}} {r}_{\mathrm{1}} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${By}\:{Pappus}−{Guldin}\:{theorem}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{V}=\mathrm{2}\pi{A}\bar {{y}}\:\:\: \\ $$$${where}\:{A}={area}\:{bounded}\:{between}\: \\ $$$${y}={r}_{\mathrm{1}} −\sqrt{{r}_{\mathrm{2}} ^{\mathrm{2}} −{x}^{\mathrm{2}} },\:{lines}\:{y}=\mathrm{0},\:{x}=\pm{r}_{\mathrm{2}} \\ $$$${and}\:\bar {{y}}={distance}\:{of}\:{centroid}\:{of}\:{A}\:{from} \\ $$$${axis}\:{of}\:{rotation}\:\left({y}=\mathrm{0}\right). \\ $$$$\therefore\:\bar {{y}}=\frac{{V}}{\mathrm{2}\pi{A}}. \\ $$$${It}\:{can}\:{be}\:{shown}\:{that}\:{A}=\frac{{r}_{\mathrm{2}} \left(\mathrm{4}{r}_{\mathrm{1}} −\pi{r}_{\mathrm{2}} \right)}{\mathrm{2}}. \\ $$$$\therefore\:\bar {{y}}=\frac{\frac{\pi{r}_{\mathrm{2}} }{\mathrm{3}}\left(\mathrm{6}{r}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{4}{r}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{3}\pi{r}_{\mathrm{1}} {r}_{\mathrm{2}} \right)}{\mathrm{2}\pi\frac{{r}_{\mathrm{2}} \left(\mathrm{4}{r}_{\mathrm{1}} −\pi{r}_{\mathrm{2}} \right)}{\mathrm{2}}} \\ $$$${or}\:\bar {{y}}=\frac{\mathrm{6}{r}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{4}{r}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{3}\pi{r}_{\mathrm{1}} {r}_{\mathrm{2}} }{\mathrm{3}\left(\mathrm{4}{r}_{\mathrm{1}} −\pi{r}_{\mathrm{2}} \right)} \\ $$$$ \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 24/Aug/16

$$\mathcal{THANKS}!\:{I}\:{am}\:{trying}\:{to}\:{understand}.\:{At}\:{the}\:{moment}\: \\ $$$${I}\:{am}\:{not}\:{much}\:{involved}\:{in}\:{analytic}\:{approach}. \\ $$
Commented by Yozzia last updated on 24/Aug/16
Commented by Yozzia last updated on 24/Aug/16

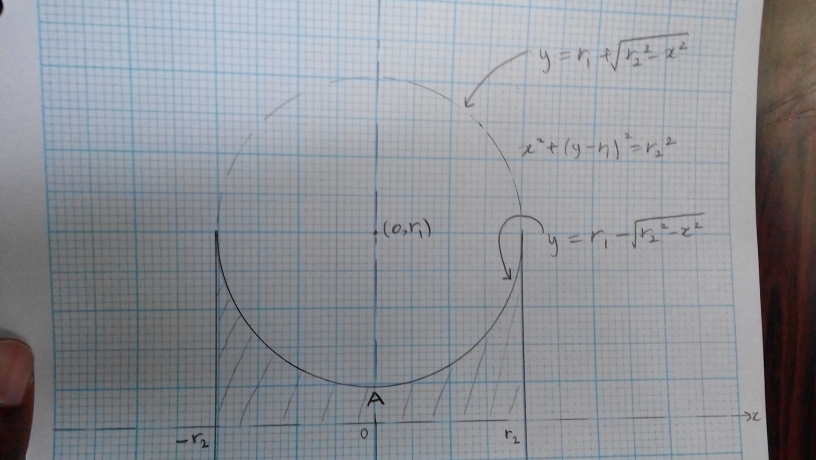
$${The}\:{volume}\:{you}\:{seek}\:{can}\:{be}\:{found} \\ $$$${by}\:{rotating}\:{the}\:{lower}\:{section}\:{of}\:{the}\: \\ $$$${circle}\:{x}^{\mathrm{2}} +\left({y}−{r}_{\mathrm{1}} \right)^{\mathrm{2}} ={r}_{\mathrm{2}} ^{\mathrm{2}} \:\:\:\mathrm{360}°\:{about} \\ $$$${the}\:{x}−{axis}.\:{I}\:{have}\:{used}\:{full}\:{ink}\:{to} \\ $$$${show}\:{the}\:{lower}\:{section}\:{and}\:{the}\:{upper} \\ $$$${section}\:{is}\:{in}\:{broken}\:{ink}. \\ $$
Commented by Rasheed Soomro last updated on 24/Aug/16

$$\mathcal{TH}\alpha{nk}\mathcal{S}\:\mathcal{A}{gain}!\:{The}\:{graph}\:{and}\:{the}\:{comment} \\ $$$${is}\:{great}\:{help}\:{in}\:{understanding}\:{your}\:{answer}! \\ $$$${I}\:{had}\:{another}\:{idea}: \\ $$$$\:\:\:\:\:{Volume}\:{of}\:{cylinder}−{semi}-{circle}\:{gape}\:{around}\: \\ $$$$\:\:\:\:\:\:{Semi}-{circle}\:{gape}=\frac{\pi{r}_{\mathrm{2}} ^{\:\mathrm{2}} }{\mathrm{2}}×{circumference}. \\ $$$${I}\:{was}\:{in}\:{confusion}\:{which}\:{circle}-{circumference} \\ $$$${should}\:{be}\:{used}.\:{Circle}\:{with}\:{radius}\:{r}_{\mathrm{1}\:} {or}\:{circle} \\ $$$${with}\:{radius}\:{r}_{\mathrm{1}} −{r}_{\mathrm{2}} \:{or}\:{average}\:{of}\:{the}\:{both}. \\ $$$${Perhaps}\:{I}\:{am}\:{not}\:{successful}\:{to}\:{clear}\:{my}\:{idea}. \\ $$
Commented by Yozzia last updated on 24/Aug/16

$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Centroid}\:{of}\:{semicircular}\:{area}\:{is}\:\frac{\mathrm{4}{r}_{\mathrm{2}} }{\mathrm{3}\pi}\:{from}\:{the}\:{center}\:{of}\:{straight}\:{edge}. \\ $$$$\therefore\:{Required}\:{distance}=\left({r}_{\mathrm{1}} −{r}_{\mathrm{2}} \right)+\left({r}_{\mathrm{2}} −\frac{\mathrm{4}{r}_{\mathrm{2}} }{\mathrm{3}\pi}\right)={r}_{\mathrm{1}} −\frac{\mathrm{4}{r}_{\mathrm{2}} }{\mathrm{3}\pi} \\ $$$${Circumference}=\mathrm{2}\pi\left({r}_{\mathrm{1}} −\frac{\mathrm{4}{r}_{\mathrm{2}} }{\mathrm{3}\pi}\right)=\mathrm{2}\pi{r}_{\mathrm{1}} −\frac{\mathrm{8}{r}_{\mathrm{2}} }{\mathrm{3}}={c} \\ $$$${volume}=\frac{\pi{r}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\pi{r}_{\mathrm{1}} −\frac{\mathrm{8}{r}_{\mathrm{2}} }{\mathrm{3}}\right)=\pi^{\mathrm{2}} {r}_{\mathrm{1}} {r}_{\mathrm{2}} ^{\mathrm{2}} −\frac{\mathrm{4}\pi{r}_{\mathrm{2}} ^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\Rightarrow{Required}\:{volume}=\mathrm{2}\pi{r}_{\mathrm{1}} ^{\mathrm{2}} {r}_{\mathrm{2}} −{c}=\mathrm{2}\pi{r}_{\mathrm{1}} ^{\mathrm{2}} {r}_{\mathrm{2}} +\frac{\mathrm{4}\pi{r}_{\mathrm{2}} ^{\mathrm{3}} }{\mathrm{3}}−\pi^{\mathrm{2}} {r}_{\mathrm{1}} {r}_{\mathrm{2}} ^{\mathrm{2}} \:\:{as}\:{was}\:{found}. \\ $$$$ \\ $$$$ \\ $$
