Question Number 66109 by Rio Michael last updated on 09/Aug/19
Commented by Rio Michael last updated on 09/Aug/19

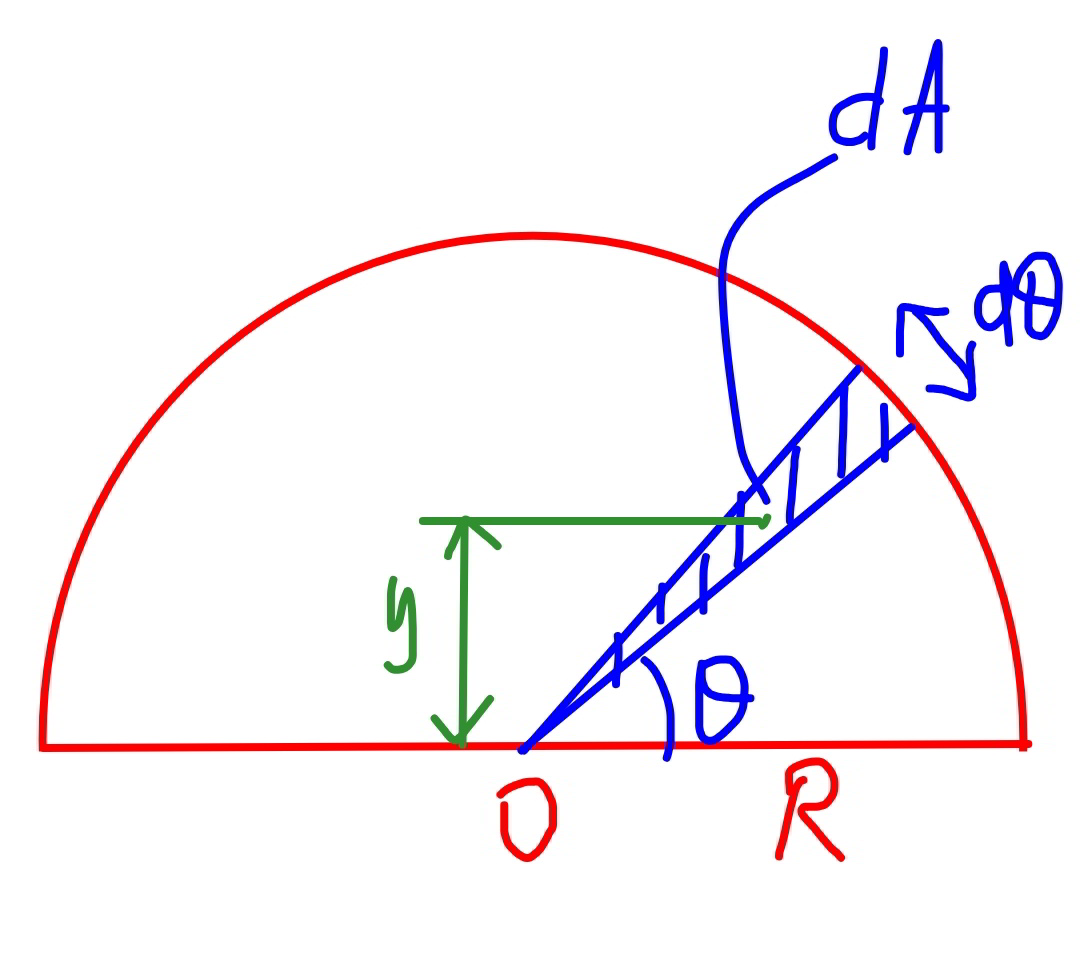
$${The}\:{diagram}\:{above}\:{shows}\:{a}\:{uniform}\:{semi}−{circular}\:{lamina}\:{of}\:{radius}\:\mathrm{2}{a} \\ $$$$,{center}\:{O}.\:{The}\:{distance}\:{of}\:{the}\:{centre}\:{of}\:{mass}\:{form}\:{P},\:{vertically}\:{above}\:{O}\:{is} \\ $$$$ \\ $$$${A}\:\:\frac{\mathrm{6}{a}\pi−\mathrm{8}{a}}{\mathrm{3}\pi} \\ $$$${B}\:\:\frac{\mathrm{6}{a}\pi\:+\:\mathrm{8}{a}}{\mathrm{3}\pi} \\ $$$${C}\:\frac{\mathrm{8}{a}−\mathrm{6}{a}\pi}{\mathrm{3}\pi} \\ $$$${D}\:\frac{\mathrm{6}{a}\pi−\mathrm{4}{a}}{\mathrm{3}\pi} \\ $$
Answered by mr W last updated on 09/Aug/19
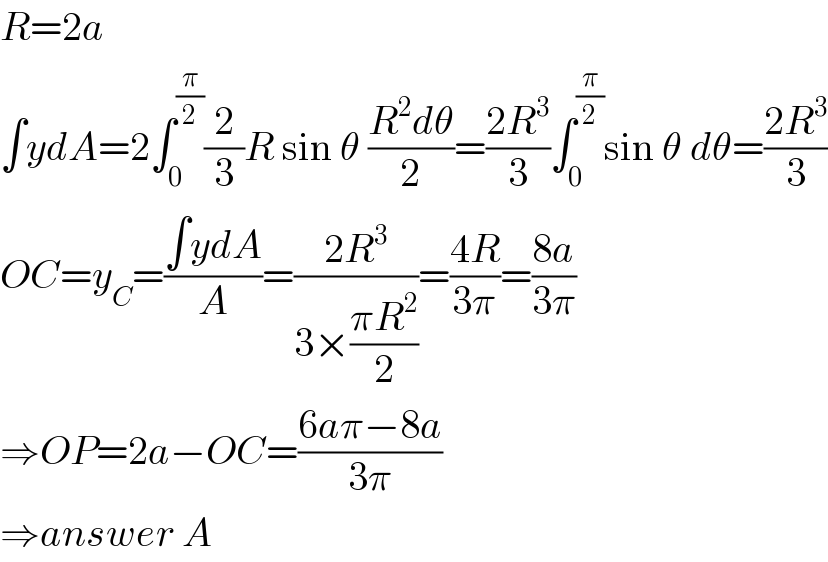
$${R}=\mathrm{2}{a} \\ $$$$\int{ydA}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}}{\mathrm{3}}{R}\:\mathrm{sin}\:\theta\:\frac{{R}^{\mathrm{2}} {d}\theta}{\mathrm{2}}=\frac{\mathrm{2}{R}^{\mathrm{3}} }{\mathrm{3}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}\:\theta\:{d}\theta=\frac{\mathrm{2}{R}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${OC}={y}_{{C}} =\frac{\int{ydA}}{{A}}=\frac{\mathrm{2}{R}^{\mathrm{3}} }{\mathrm{3}×\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}}=\frac{\mathrm{4}{R}}{\mathrm{3}\pi}=\frac{\mathrm{8}{a}}{\mathrm{3}\pi} \\ $$$$\Rightarrow{OP}=\mathrm{2}{a}−{OC}=\frac{\mathrm{6}{a}\pi−\mathrm{8}{a}}{\mathrm{3}\pi} \\ $$$$\Rightarrow{answer}\:{A} \\ $$
Commented by mr W last updated on 10/Aug/19