Question Number 138564 by DomaPeti last updated on 14/Apr/21
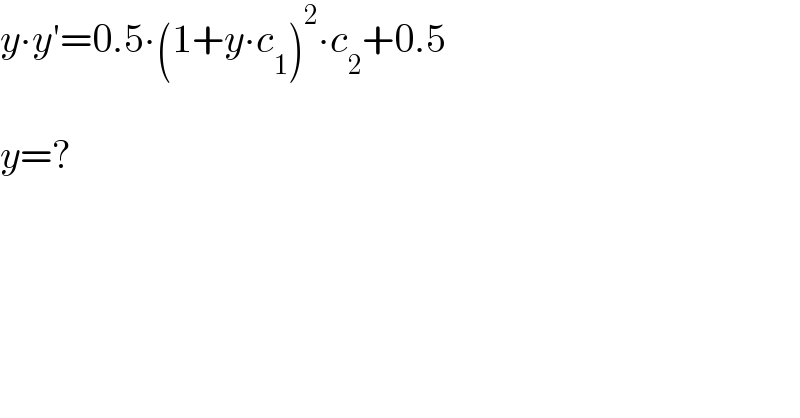
$${y}\centerdot{y}'=\mathrm{0}.\mathrm{5}\centerdot\left(\mathrm{1}+{y}\centerdot{c}_{\mathrm{1}} \right)^{\mathrm{2}} \centerdot{c}_{\mathrm{2}} +\mathrm{0}.\mathrm{5} \\ $$$$ \\ $$$${y}=? \\ $$
Answered by mr W last updated on 15/Apr/21

$$\mathrm{2}{yy}'={c}_{\mathrm{2}} \left(\mathrm{1}+{c}_{\mathrm{1}} {y}\right)^{\mathrm{2}} +\mathrm{1}={c}_{\mathrm{2}} {c}_{\mathrm{1}} ^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{2}{c}_{\mathrm{1}} {c}_{\mathrm{2}} {y}+{c}_{\mathrm{2}} +\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={ay}^{\mathrm{2}} +{by}+{c} \\ $$$$\int\frac{\mathrm{2}{ydy}}{{ay}^{\mathrm{2}} +{by}+{c}}=\int{dx} \\ $$$${x}=\int\frac{\mathrm{2}{ydy}}{{ay}^{\mathrm{2}} +{by}+{c}} \\ $$$$… \\ $$
Commented by mr W last updated on 15/Apr/21

Commented by ArielVyny last updated on 15/Apr/21

$${for}\:\int\frac{\mathrm{1}}{\left({dx}+{e}\right)\sqrt{{ax}^{\mathrm{2}} +{bx}+{c}}}{dx}=?? \\ $$$$ \\ $$
Commented by mr W last updated on 16/Apr/21

$${please}\:{open}\:{a}\:{new}\:{thread}\:{for}\:{your} \\ $$$${question}. \\ $$
