Question Number 73040 by mathmax by abdo last updated on 05/Nov/19
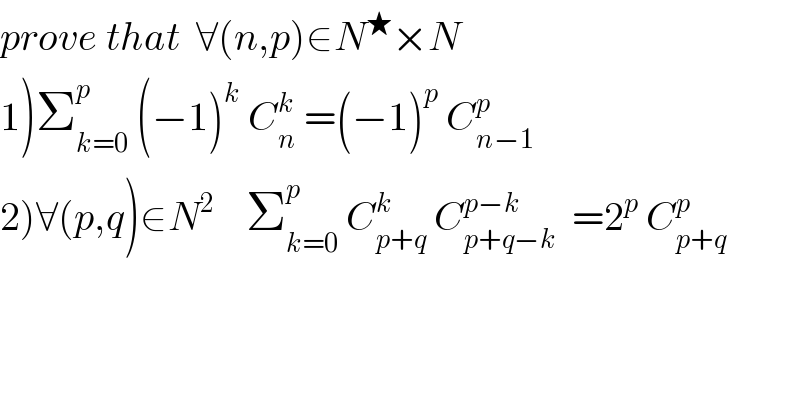
$${prove}\:{that}\:\:\forall\left({n},{p}\right)\in{N}^{\bigstar} ×{N} \\ $$$$\left.\mathrm{1}\right)\sum_{{k}=\mathrm{0}} ^{{p}} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{{n}} ^{{k}} \:=\left(−\mathrm{1}\right)^{{p}} \:{C}_{{n}−\mathrm{1}} ^{{p}} \\ $$$$\left.\mathrm{2}\right)\forall\left({p},{q}\right)\in{N}^{\mathrm{2}} \:\:\:\:\sum_{{k}=\mathrm{0}} ^{{p}} \:{C}_{{p}+{q}} ^{{k}} \:{C}_{{p}+{q}−{k}} ^{{p}−{k}} \:\:=\mathrm{2}^{{p}} \:{C}_{{p}+{q}} ^{{p}} \\ $$
Answered by mind is power last updated on 06/Nov/19
![1) recursion 2 nd lets A=[1,,,p+q] in A we can get C_(p+q) ^p set withe p elements the number of idont now the nam in inglish ′′A={1,2}/P(A)={∅,{1},{2},{1,2}}′′ if A is card p⇒P(A)=2^p sl the number all partition of set withe p element is 2^p C_(p+q) ^p we can chose this element we pick k element in p+q and p−k in p+q−k ⇒=Σ_(k=0) ^p C_(p+q) ^k C_(p+q−k) ^(p−k) =2^p C_(p+q) ^p](https://www.tinkutara.com/question/Q73094.png)
$$\left.\mathrm{1}\right)\:\mathrm{recursion} \\ $$$$\mathrm{2}\:\mathrm{nd} \\ $$$$\mathrm{lets}\:\mathrm{A}=\left[\mathrm{1},,,\mathrm{p}+\mathrm{q}\right] \\ $$$$\mathrm{in}\:\mathrm{A}\:\mathrm{we}\:\mathrm{can}\:\mathrm{get} \\ $$$$\mathrm{C}_{\mathrm{p}+\mathrm{q}} ^{\mathrm{p}} \:\mathrm{set}\:\mathrm{withe}\:\mathrm{p}\:\mathrm{elements} \\ $$$$\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{idont}\:\mathrm{now}\:\mathrm{the}\:\mathrm{nam}\:\mathrm{in}\:\mathrm{inglish} \\ $$$$''\mathrm{A}=\left\{\mathrm{1},\mathrm{2}\right\}/\mathrm{P}\left(\mathrm{A}\right)=\left\{\varnothing,\left\{\mathrm{1}\right\},\left\{\mathrm{2}\right\},\left\{\mathrm{1},\mathrm{2}\right\}\right\}'' \\ $$$$\mathrm{if}\:\mathrm{A}\:\mathrm{is}\:\mathrm{card}\:\mathrm{p}\Rightarrow\mathrm{P}\left(\mathrm{A}\right)=\mathrm{2}^{\mathrm{p}} \\ $$$$\mathrm{sl}\:\mathrm{the}\:\mathrm{number}\:\mathrm{all}\:\mathrm{partition}\:\mathrm{of}\:\mathrm{set}\:\mathrm{withe}\:\mathrm{p}\:\mathrm{element}\:\mathrm{is}\:\mathrm{2}^{\mathrm{p}} \mathrm{C}_{\mathrm{p}+\mathrm{q}} ^{\mathrm{p}} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{chose}\:\mathrm{this}\:\mathrm{element} \\ $$$$\mathrm{we}\:\mathrm{pick}\:\mathrm{k}\:\mathrm{element}\:\mathrm{in}\:\mathrm{p}+\mathrm{q} \\ $$$$\mathrm{and}\:\:\:\:\mathrm{p}−\mathrm{k}\:\mathrm{in}\:\:\mathrm{p}+\mathrm{q}−\mathrm{k}\: \\ $$$$\Rightarrow=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{p}} {\sum}}\mathrm{C}_{\mathrm{p}+\mathrm{q}} ^{\mathrm{k}} \mathrm{C}_{\mathrm{p}+\mathrm{q}−\mathrm{k}} ^{\mathrm{p}−\mathrm{k}} =\mathrm{2}^{\mathrm{p}} \mathrm{C}_{\mathrm{p}+\mathrm{q}} ^{\mathrm{p}} \\ $$
