Menu Close

let-P-n-X-n-X-n-1-X-2-X-1-R-X-1-prove-that-P-n-have-one-root-x-n-inside-0-2-study-the-sequence-x-n-

Tinku Tara 0 Comments
Pin




Question Number 73052 by mathmax by abdo last updated on 05/Nov/19
let P_n =X^n +X^(n−1) +....+X^2 +X−1 ∈R[X] 1)prove that P_n have one root x_n inside ]0,+∞[ 2)study the sequence x_n
$${let}\:{P}_{{n}} ={X}^{{n}} \:+{X}^{{n}−\mathrm{1}} \:+….+{X}^{\mathrm{2}} \:+{X}−\mathrm{1}\:\in{R}\left[{X}\right] \\ $$$$\left.\mathrm{1}\left.\right){prove}\:{that}\:{P}_{{n}} {have}\:{one}\:{root}\:{x}_{{n}} \:{inside}\:\right]\mathrm{0},+\infty\left[\right. \\ $$$$\left.\mathrm{2}\right){study}\:{the}\:{sequence}\:{x}_{{n}} \\ $$
Answered by mind is power last updated on 06/Nov/19
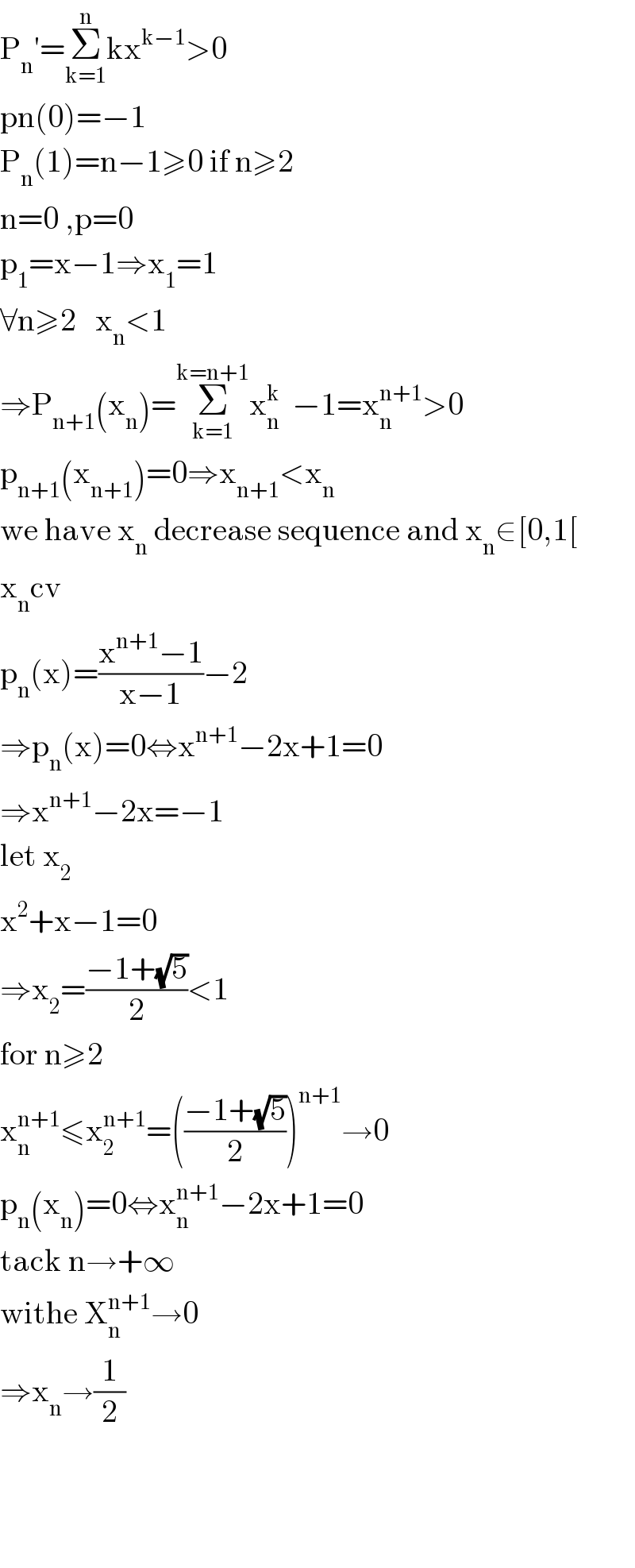
P_n ′=Σ_(k=1) ^n kx^(k−1) >0 pn(0)=−1 P_n (1)=n−1≥0 if n≥2 n=0 ,p=0 p_1 =x−1⇒x_1 =1 ∀n≥2 x_n <1 ⇒P_(n+1) (x_n )=Σ_(k=1) ^(k=n+1) x_n ^k −1=x_n ^(n+1) >0 p_(n+1) (x_(n+1) )=0⇒x_(n+1) <x_n we have x_n decrease sequence and x_n ∈[0,1[ x_n cv p_n (x)=((x^(n+1) −1)/(x−1))−2 ⇒p_n (x)=0⇔x^(n+1) −2x+1=0 ⇒x^(n+1) −2x=−1 let x_2 x^2 +x−1=0 ⇒x_2 =((−1+(√5))/2)<1 for n≥2 x_n ^(n+1) ≤x_2 ^(n+1) =(((−1+(√5))/2))^(n+1) →0 p_n (x_n )=0⇔x_n ^(n+1) −2x+1=0 tack n→+∞ withe X_n ^(n+1) →0 ⇒x_n →(1/2)
$$\mathrm{P}_{\mathrm{n}} '=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{kx}^{\mathrm{k}−\mathrm{1}} >\mathrm{0} \\ $$$$\mathrm{pn}\left(\mathrm{0}\right)=−\mathrm{1} \\ $$$$\mathrm{P}_{\mathrm{n}} \left(\mathrm{1}\right)=\mathrm{n}−\mathrm{1}\geqslant\mathrm{0}\:\mathrm{if}\:\mathrm{n}\geqslant\mathrm{2} \\ $$$$\mathrm{n}=\mathrm{0}\:,\mathrm{p}=\mathrm{0} \\ $$$$\mathrm{p}_{\mathrm{1}} =\mathrm{x}−\mathrm{1}\Rightarrow\mathrm{x}_{\mathrm{1}} =\mathrm{1} \\ $$$$\forall\mathrm{n}\geqslant\mathrm{2}\:\:\:\mathrm{x}_{\mathrm{n}} <\mathrm{1} \\ $$$$\Rightarrow\mathrm{P}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{x}_{\mathrm{n}} \right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{k}=\mathrm{n}+\mathrm{1}} {\sum}}\mathrm{x}_{\mathrm{n}} ^{\mathrm{k}} \:\:−\mathrm{1}=\mathrm{x}_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} >\mathrm{0} \\ $$$$\mathrm{p}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{x}_{\mathrm{n}+\mathrm{1}} \right)=\mathrm{0}\Rightarrow\mathrm{x}_{\mathrm{n}+\mathrm{1}} <\mathrm{x}_{\mathrm{n}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{x}_{\mathrm{n}} \:\mathrm{decrease}\:\mathrm{sequence}\:\mathrm{and}\:\mathrm{x}_{\mathrm{n}} \in\left[\mathrm{0},\mathrm{1}\left[\right.\right. \\ $$$$\mathrm{x}_{\mathrm{n}} \mathrm{cv} \\ $$$$\mathrm{p}_{\mathrm{n}} \left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{x}−\mathrm{1}}−\mathrm{2} \\ $$$$\Rightarrow\mathrm{p}_{\mathrm{n}} \left(\mathrm{x}\right)=\mathrm{0}\Leftrightarrow\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{2x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{2x}=−\mathrm{1} \\ $$$$\mathrm{let}\:\mathrm{x}_{\mathrm{2}} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{2}} =\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}<\mathrm{1} \\ $$$$\mathrm{for}\:\mathrm{n}\geqslant\mathrm{2} \\ $$$$\mathrm{x}_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} \leqslant\mathrm{x}_{\mathrm{2}} ^{\mathrm{n}+\mathrm{1}} =\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{n}+\mathrm{1}} \rightarrow\mathrm{0} \\ $$$$\mathrm{p}_{\mathrm{n}} \left(\mathrm{x}_{\mathrm{n}} \right)=\mathrm{0}\Leftrightarrow\mathrm{x}_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} −\mathrm{2x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{tack}\:\mathrm{n}\rightarrow+\infty \\ $$$$\mathrm{withe}\:\mathrm{X}_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} \rightarrow\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}_{\mathrm{n}} \rightarrow\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *