Question Number 591 by 112358 last updated on 04/Feb/15

$${Prove}\:{by}\:{induction}\:{on}\:{n},\:{for}\:{n}\geqslant\mathrm{2}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{u}_{{n}} \:\geqslant\:\mathrm{2}^{\mathrm{3}^{{n}−\mathrm{1}} } \\ $$$${for}\:{the}\:{sequence}\:\left\{{u}_{{n}} \right\}\:{defined}\:{by}\: \\ $$$${the}\:{recurrence}\:{relation} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{u}_{\mathrm{1}} =\mathrm{1}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{u}_{{n}+\mathrm{1}} =\left({u}_{{n}} +\frac{\mathrm{1}}{{u}_{{n}} }\right)^{\mathrm{3}} \:\:,\:{n}\geqslant\mathrm{1}\:. \\ $$
Answered by prakash jain last updated on 04/Feb/15
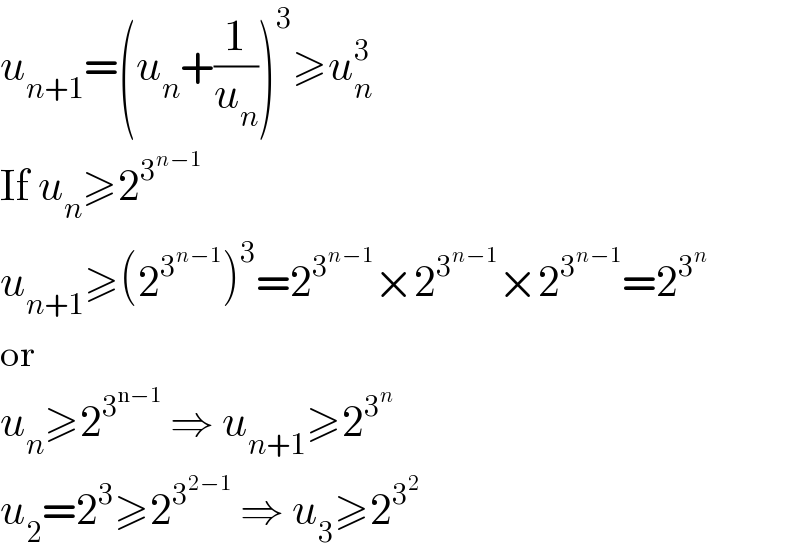
$${u}_{{n}+\mathrm{1}} =\left({u}_{{n}} +\frac{\mathrm{1}}{{u}_{{n}} }\right)^{\mathrm{3}} \geqslant{u}_{{n}} ^{\mathrm{3}} \\ $$$$\mathrm{If}\:{u}_{{n}} \geqslant\mathrm{2}^{\mathrm{3}^{{n}−\mathrm{1}} } \\ $$$${u}_{{n}+\mathrm{1}} \geqslant\left(\mathrm{2}^{\mathrm{3}^{{n}−\mathrm{1}} } \right)^{\mathrm{3}} =\mathrm{2}^{\mathrm{3}^{{n}−\mathrm{1}} } ×\mathrm{2}^{\mathrm{3}^{{n}−\mathrm{1}} } ×\mathrm{2}^{\mathrm{3}^{{n}−\mathrm{1}} } =\mathrm{2}^{\mathrm{3}^{{n}} } \\ $$$$\mathrm{or} \\ $$$${u}_{{n}} \geqslant\mathrm{2}^{\mathrm{3}^{\mathrm{n}−\mathrm{1}} } \:\Rightarrow\:{u}_{{n}+\mathrm{1}} \geqslant\mathrm{2}^{\mathrm{3}^{{n}} } \\ $$$${u}_{\mathrm{2}} =\mathrm{2}^{\mathrm{3}} \geqslant\mathrm{2}^{\mathrm{3}^{\mathrm{2}−\mathrm{1}} } \:\Rightarrow\:{u}_{\mathrm{3}} \geqslant\mathrm{2}^{\mathrm{3}^{\mathrm{2}} } \\ $$
