Question Number 597 by 112358 last updated on 08/Feb/15
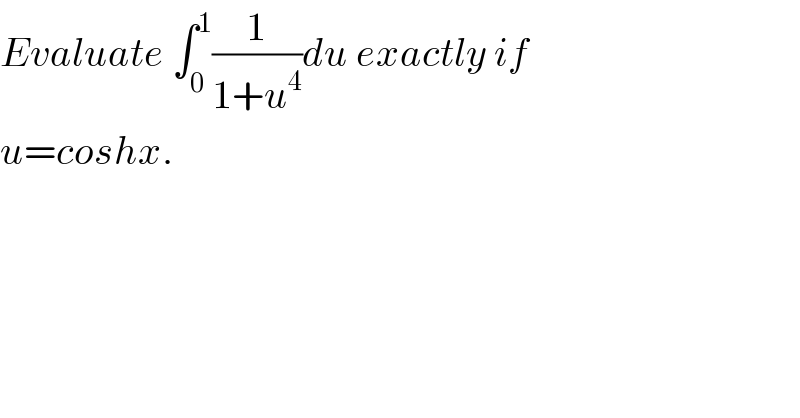
$${Evaluate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{4}} }{du}\:{exactly}\:{if}\: \\ $$$${u}={coshx}.\: \\ $$
Commented by prakash jain last updated on 08/Feb/15
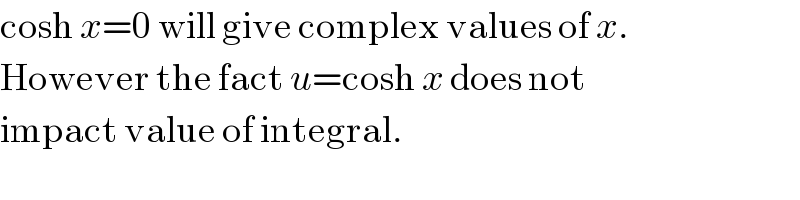
$$\mathrm{cosh}\:{x}=\mathrm{0}\:\mathrm{will}\:\mathrm{give}\:\mathrm{complex}\:\mathrm{values}\:\mathrm{of}\:{x}. \\ $$$$\mathrm{However}\:\mathrm{the}\:\mathrm{fact}\:{u}=\mathrm{cosh}\:{x}\:\mathrm{does}\:\mathrm{not} \\ $$$$\mathrm{impact}\:\mathrm{value}\:\mathrm{of}\:\mathrm{integral}. \\ $$
Answered by prakash jain last updated on 08/Feb/15
![1+u^4 =(u^2 +1)^2 −2u^2 =(u^2 +(√2)u+1)(u^2 −(√2)u+1) (1/(1+u^4 ))=((Au+B)/(u^2 +(√2)u+1))+((Cu+D)/(u^2 −(√2)u+1)) (A+C)u^3 +(B+D−(√2)A+(√2)C)u^2 +(A+C+D(√2)−B(√2))u +(B+D)=1 A+C=0 ⇒A=−C ....(i) B+D−A(√2)+C(√2)=0 ...(ii) A+C+D(√2)−B(√2)=0 ⇒B=D ...(iii) B+D=1 ...(iv) From (i), (ii) and (iv) 1+C(√2)+C(√2)=0⇒C=((−1)/(2(√2)))⇒A=(1/(2(√2))) From (iii) and (iv) B=(1/2), D=(1/2) (1/(1+u^4 ))=(((1/(2(√2)))u+(1/2))/(u^2 +(√2)u+1)) +((((−1)/(2(√2)))u+(1/2))/(u^2 −(√2)u+1)) =(1/(2(√2)))[((u+(√2))/(u^2 +u(√2)+1)) −((u−(√2))/(u^2 −u(√2)+1))] =(1/(4(√2)))[((2u+(√2))/(u^2 +u(√2)+1))+((√2)/(u^2 +u(√2)+1))−((2u−(√2))/(u^2 −u(√2)+1))−((√2)/(u^2 −u(√2)+1)) ∫((2u+(√2))/(u^2 +u(√2)+1))du=ln (u^2 +u(√2)+1) ∫((2u+(√2))/(u^2 −u(√2)+1))du=ln (u^2 −u(√2)+1) ∫(1/(u^2 +u(√2)+1))du=∫ (1/(u^2 +u(√2)+(1/2)+(1/2)))du =∫(1/((u+(1/( (√2))))^2 +((1/( (√2))))^2 )) du=(√2) arctan ((u+(1/( (√2))))/(1/( (√2))))=(√2)arctan(u(√2)+1) ∫(1/(u^2 −u(√2)+1))du=∫ (1/(u^2 −u(√2)+(1/2)+(1/2)))du = =(√2)arctan (u(√2)−1) Putting all integrals together ∫(1/(1+u^4 ))du= (1/(4(√2)))[ln (u^2 +u(√2)+1)−ln (u^2 −u(√2)+1)+2arctan(u(√2)+1)−2arctan (u(√2)−1)] =(1/(4(√2)))[ln ((u^2 +u(√2)+1)/(u^2 −u(√2)+1))+2arctan (u(√2)+1)−2arctan (u(√2)−1) Value at u=1 (1/(4(√2)))[ln ((2+(√2))/(2−(√2)))+2arctan ((√2)+1)−2arctan ((√2)−1)] Value at u=0 (1/(4(√2)))[ln 1+2arctan 1−2arctan (−1)]=(π/(4(√2)))](https://www.tinkutara.com/question/Q598.png)
$$\mathrm{1}+{u}^{\mathrm{4}} =\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}{u}^{\mathrm{2}} =\left({u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}+\mathrm{1}\right)\left({u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}+\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{4}} }=\frac{{Au}+{B}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}+\mathrm{1}}+\frac{{Cu}+{D}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}+\mathrm{1}} \\ $$$$\left({A}+{C}\right){u}^{\mathrm{3}} +\left({B}+{D}−\sqrt{\mathrm{2}}{A}+\sqrt{\mathrm{2}}{C}\right){u}^{\mathrm{2}} +\left({A}+{C}+{D}\sqrt{\mathrm{2}}−{B}\sqrt{\mathrm{2}}\right){u} \\ $$$$\:\:\:\:+\left({B}+{D}\right)=\mathrm{1} \\ $$$${A}+{C}=\mathrm{0}\:\:\:\:\Rightarrow{A}=−{C}\:….\left(\mathrm{i}\right) \\ $$$${B}+{D}−{A}\sqrt{\mathrm{2}}+{C}\sqrt{\mathrm{2}}=\mathrm{0}\:\:\:\:\:\:…\left(\mathrm{ii}\right) \\ $$$${A}+{C}+{D}\sqrt{\mathrm{2}}−{B}\sqrt{\mathrm{2}}=\mathrm{0}\:\:\:\:\:\Rightarrow{B}={D}\:…\left(\mathrm{iii}\right) \\ $$$${B}+{D}=\mathrm{1}\:\:\:\:\:\:…\left(\mathrm{iv}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{i}\right),\:\left(\mathrm{ii}\right)\:\mathrm{and}\:\left(\mathrm{iv}\right) \\ $$$$\mathrm{1}+{C}\sqrt{\mathrm{2}}+{C}\sqrt{\mathrm{2}}=\mathrm{0}\Rightarrow{C}=\frac{−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\Rightarrow{A}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{From}\:\left(\mathrm{iii}\right)\:\mathrm{and}\:\left(\mathrm{iv}\right) \\ $$$${B}=\frac{\mathrm{1}}{\mathrm{2}},\:{D}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{4}} }=\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{u}+\frac{\mathrm{1}}{\mathrm{2}}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}+\mathrm{1}}\:+\frac{\frac{−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{u}+\frac{\mathrm{1}}{\mathrm{2}}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}+\mathrm{1}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left[\frac{{u}+\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} +{u}\sqrt{\mathrm{2}}+\mathrm{1}}\:−\frac{{u}−\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} −{u}\sqrt{\mathrm{2}}+\mathrm{1}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[\frac{\mathrm{2}{u}+\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} +{u}\sqrt{\mathrm{2}}+\mathrm{1}}+\frac{\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} +{u}\sqrt{\mathrm{2}}+\mathrm{1}}−\frac{\mathrm{2}{u}−\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} −{u}\sqrt{\mathrm{2}}+\mathrm{1}}−\frac{\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} −{u}\sqrt{\mathrm{2}}+\mathrm{1}}\right. \\ $$$$\int\frac{\mathrm{2}{u}+\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} +{u}\sqrt{\mathrm{2}}+\mathrm{1}}{du}=\mathrm{ln}\:\left({u}^{\mathrm{2}} +{u}\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$$$\int\frac{\mathrm{2}{u}+\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} −{u}\sqrt{\mathrm{2}}+\mathrm{1}}{du}=\mathrm{ln}\:\left({u}^{\mathrm{2}} −{u}\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$$$\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} +{u}\sqrt{\mathrm{2}}+\mathrm{1}}{du}=\int\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} +{u}\sqrt{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}}{du}\: \\ $$$$\:\:\:\:=\int\frac{\mathrm{1}}{\left({u}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }\:{du}=\sqrt{\mathrm{2}}\:\mathrm{arctan}\:\frac{{u}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}=\sqrt{\mathrm{2}}\mathrm{arctan}\left({u}\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$$$\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} −{u}\sqrt{\mathrm{2}}+\mathrm{1}}{du}=\int\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} −{u}\sqrt{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}}{du}\:= \\ $$$$\:\:\:\:\:\:\:\:=\sqrt{\mathrm{2}}\mathrm{arctan}\:\left({u}\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\mathrm{Putting}\:\mathrm{all}\:\mathrm{integrals}\:\mathrm{together} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{4}} }{du}= \\ $$$$\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[\mathrm{ln}\:\left({u}^{\mathrm{2}} +{u}\sqrt{\mathrm{2}}+\mathrm{1}\right)−\mathrm{ln}\:\left({u}^{\mathrm{2}} −{u}\sqrt{\mathrm{2}}+\mathrm{1}\right)+\mathrm{2arctan}\left({u}\sqrt{\mathrm{2}}+\mathrm{1}\right)−\mathrm{2arctan}\:\left({u}\sqrt{\mathrm{2}}−\mathrm{1}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[\mathrm{ln}\:\frac{{u}^{\mathrm{2}} +{u}\sqrt{\mathrm{2}}+\mathrm{1}}{{u}^{\mathrm{2}} −{u}\sqrt{\mathrm{2}}+\mathrm{1}}+\mathrm{2arctan}\:\left({u}\sqrt{\mathrm{2}}+\mathrm{1}\right)−\mathrm{2arctan}\:\left({u}\sqrt{\mathrm{2}}−\mathrm{1}\right)\right. \\ $$$$\mathrm{Value}\:\mathrm{at}\:{u}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[\mathrm{ln}\:\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}−\sqrt{\mathrm{2}}}+\mathrm{2arctan}\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)−\mathrm{2arctan}\:\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\right] \\ $$$$\mathrm{Value}\:\mathrm{at}\:{u}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[\mathrm{ln}\:\mathrm{1}+\mathrm{2arctan}\:\mathrm{1}−\mathrm{2arctan}\:\left(−\mathrm{1}\right)\right]=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$
