Question Number 604 by 123456 last updated on 09/Feb/15
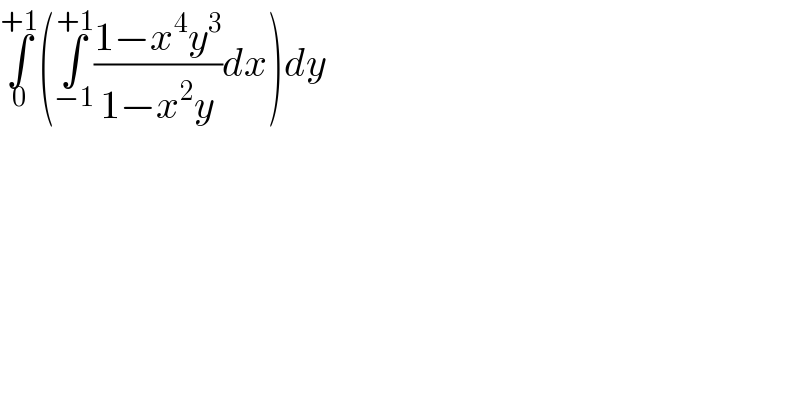
$$\underset{\mathrm{0}} {\overset{+\mathrm{1}} {\int}}\left(\underset{−\mathrm{1}} {\overset{+\mathrm{1}} {\int}}\frac{\mathrm{1}−{x}^{\mathrm{4}} {y}^{\mathrm{3}} }{\mathrm{1}−{x}^{\mathrm{2}} {y}}{dx}\right){dy} \\ $$
Answered by prakash jain last updated on 15/Feb/15
![((1−x^4 y^3 )/(1−x^2 y))=((x^2 y^2 −x^4 y^3 −x^2 y^2 +y+1−y)/(1−x^2 y)) =((x^2 y^2 (1−x^2 y)+y(1−x^2 y)+(1−y))/(1−x^2 y)) =x^2 y^2 +y+((1−y)/(1−x^2 y)) Integrate wrt x ((y^2 x^3 )/3)+xy+((1−y)/( (√y)))tanh^(−1) (x(√y)) putting limits =((2y^2 )/3)+2y+2((1−y)/( (√y)))tanh^(−1) ((√y)) I1 ∫_0 ^1 ((2y^2 )/3)dy=[((2y^3 )/9)]_0 ^1 =(2/9) I2 ∫_0 ^1 2y dy=[y^2 ]_0 ^1 =1 I3 ∫_0 ^1 2((1−y)/( (√y)))tanh^(−1) ((√y))dy y=u^2 ⇒dy=2udu ∫_0 ^1 2((1−u^2 )/u)tanh^(−1) u 2udu =4∫_0 ^1 (1−u^2 )tanh^(−1) u du =4[ln 2−(1/3)ln 2−(1/6)] =(8/3)ln 2−(2/3) Final Answer (2/9)+1+(8/3)ln 2−(2/3) =(8/3)ln 2+((2+9−6)/9)=(8/3)ln 2+(5/9)](https://www.tinkutara.com/question/Q607.png)
$$\frac{\mathrm{1}−{x}^{\mathrm{4}} {y}^{\mathrm{3}} }{\mathrm{1}−{x}^{\mathrm{2}} {y}}=\frac{{x}^{\mathrm{2}} {y}^{\mathrm{2}} −{x}^{\mathrm{4}} {y}^{\mathrm{3}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}+\mathrm{1}−{y}}{\mathrm{1}−{x}^{\mathrm{2}} {y}} \\ $$$$=\frac{{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} {y}\right)+{y}\left(\mathrm{1}−{x}^{\mathrm{2}} {y}\right)+\left(\mathrm{1}−{y}\right)}{\mathrm{1}−{x}^{\mathrm{2}} {y}} \\ $$$$={x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}+\frac{\mathrm{1}−{y}}{\mathrm{1}−{x}^{\mathrm{2}} {y}} \\ $$$$\mathrm{Integrate}\:\mathrm{wrt}\:{x} \\ $$$$\frac{{y}^{\mathrm{2}} {x}^{\mathrm{3}} }{\mathrm{3}}+{xy}+\frac{\mathrm{1}−{y}}{\:\sqrt{{y}}}\mathrm{tanh}^{−\mathrm{1}} \left({x}\sqrt{{y}}\right) \\ $$$$\mathrm{putting}\:\mathrm{limits} \\ $$$$=\frac{\mathrm{2}{y}^{\mathrm{2}} }{\mathrm{3}}+\mathrm{2}{y}+\mathrm{2}\frac{\mathrm{1}−{y}}{\:\sqrt{{y}}}\mathrm{tanh}^{−\mathrm{1}} \left(\sqrt{\mathrm{y}}\right) \\ $$$$\mathrm{I1} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{y}^{\mathrm{2}} }{\mathrm{3}}{dy}=\left[\frac{\mathrm{2}{y}^{\mathrm{3}} }{\mathrm{9}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{9}} \\ $$$$\mathrm{I2} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{2}{y}\:{dy}=\left[{y}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{I3} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}\frac{\mathrm{1}−{y}}{\:\sqrt{{y}}}\mathrm{tanh}^{−\mathrm{1}} \left(\sqrt{\mathrm{y}}\right){dy} \\ $$$${y}={u}^{\mathrm{2}} \:\Rightarrow{dy}=\mathrm{2}{udu} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}\frac{\mathrm{1}−{u}^{\mathrm{2}} }{{u}}\mathrm{tanh}^{−\mathrm{1}} {u}\:\mathrm{2}{udu} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}^{\mathrm{2}} \right)\mathrm{tanh}^{−\mathrm{1}} {u}\:{du} \\ $$$$=\mathrm{4}\left[\mathrm{ln}\:\mathrm{2}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mathrm{2}−\frac{\mathrm{1}}{\mathrm{6}}\right] \\ $$$$=\frac{\mathrm{8}}{\mathrm{3}}\mathrm{ln}\:\mathrm{2}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{Final}\:\mathrm{Answer} \\ $$$$\frac{\mathrm{2}}{\mathrm{9}}+\mathrm{1}+\frac{\mathrm{8}}{\mathrm{3}}\mathrm{ln}\:\mathrm{2}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{8}}{\mathrm{3}}\mathrm{ln}\:\mathrm{2}+\frac{\mathrm{2}+\mathrm{9}−\mathrm{6}}{\mathrm{9}}=\frac{\mathrm{8}}{\mathrm{3}}\mathrm{ln}\:\mathrm{2}+\frac{\mathrm{5}}{\mathrm{9}} \\ $$
