Question Number 73251 by aliesam last updated on 09/Nov/19
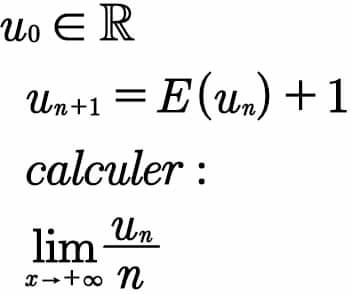
Answered by mind is power last updated on 09/Nov/19
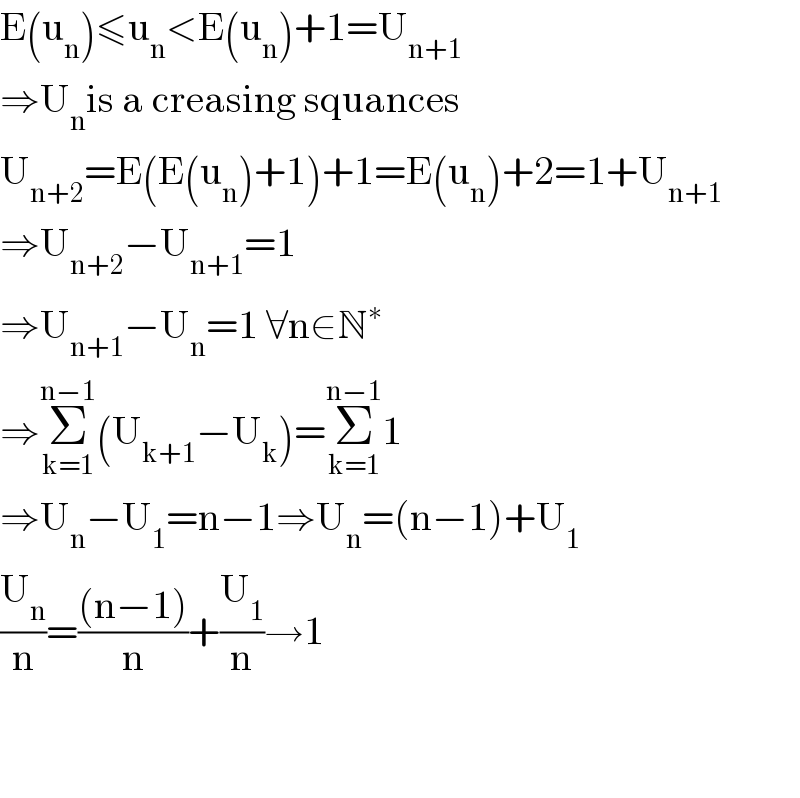
$$\mathrm{E}\left(\mathrm{u}_{\mathrm{n}} \right)\leqslant\mathrm{u}_{\mathrm{n}} <\mathrm{E}\left(\mathrm{u}_{\mathrm{n}} \right)+\mathrm{1}=\mathrm{U}_{\mathrm{n}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{U}_{\mathrm{n}} \mathrm{is}\:\mathrm{a}\:\mathrm{creasing}\:\mathrm{squances} \\ $$$$\mathrm{U}_{\mathrm{n}+\mathrm{2}} =\mathrm{E}\left(\mathrm{E}\left(\mathrm{u}_{\mathrm{n}} \right)+\mathrm{1}\right)+\mathrm{1}=\mathrm{E}\left(\mathrm{u}_{\mathrm{n}} \right)+\mathrm{2}=\mathrm{1}+\mathrm{U}_{\mathrm{n}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{U}_{\mathrm{n}+\mathrm{2}} −\mathrm{U}_{\mathrm{n}+\mathrm{1}} =\mathrm{1} \\ $$$$\Rightarrow\mathrm{U}_{\mathrm{n}+\mathrm{1}} −\mathrm{U}_{\mathrm{n}} =\mathrm{1}\:\forall\mathrm{n}\in\mathbb{N}^{\ast} \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\left(\mathrm{U}_{\mathrm{k}+\mathrm{1}} −\mathrm{U}_{\mathrm{k}} \right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{1} \\ $$$$\Rightarrow\mathrm{U}_{\mathrm{n}} −\mathrm{U}_{\mathrm{1}} =\mathrm{n}−\mathrm{1}\Rightarrow\mathrm{U}_{\mathrm{n}} =\left(\mathrm{n}−\mathrm{1}\right)+\mathrm{U}_{\mathrm{1}} \\ $$$$\frac{\mathrm{U}_{\mathrm{n}} }{\mathrm{n}}=\frac{\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{n}}+\frac{\mathrm{U}_{\mathrm{1}} }{\mathrm{n}}\rightarrow\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
