Question Number 7752 by Tawakalitu. last updated on 14/Sep/16
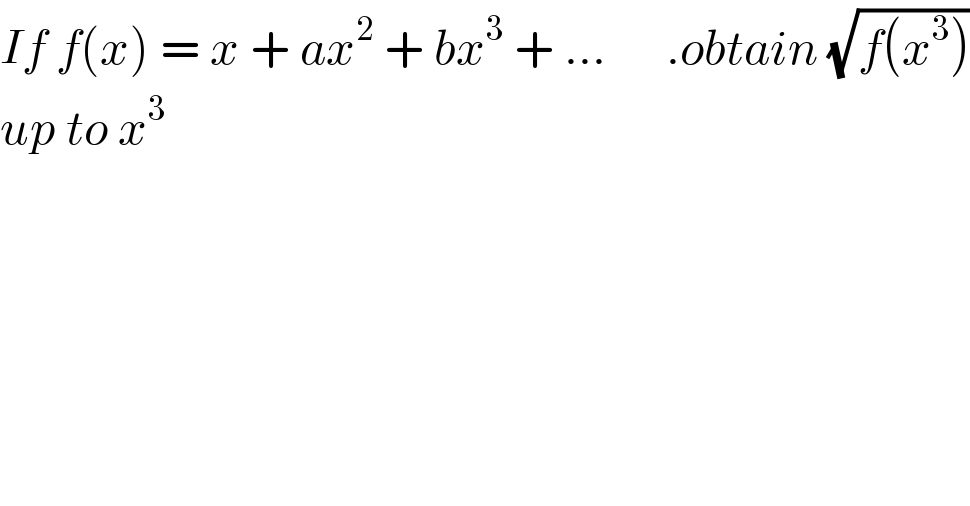
$${If}\:{f}\left({x}\right)\:=\:{x}\:+\:{ax}^{\mathrm{2}} \:+\:{bx}^{\mathrm{3}} \:+\:…\:\:\:\:\:\:.{obtain}\:\sqrt{{f}\left({x}^{\mathrm{3}} \right)} \\ $$$${up}\:{to}\:{x}^{\mathrm{3}} \\ $$
Commented by FilupSmith last updated on 14/Sep/16
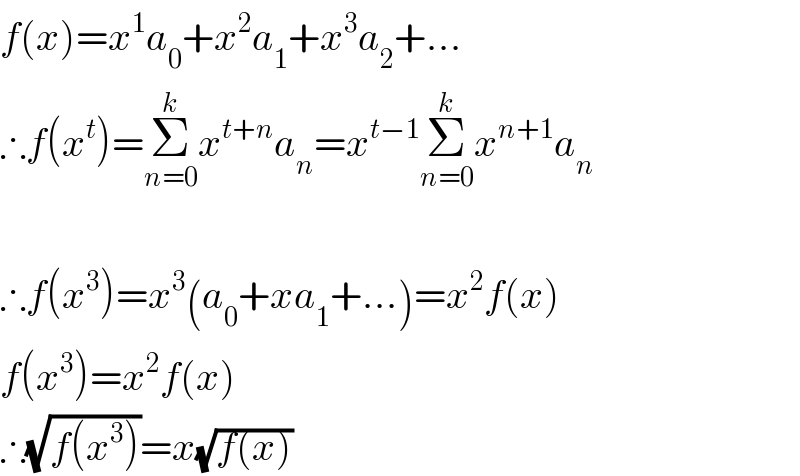
$${f}\left({x}\right)={x}^{\mathrm{1}} {a}_{\mathrm{0}} +{x}^{\mathrm{2}} {a}_{\mathrm{1}} +{x}^{\mathrm{3}} {a}_{\mathrm{2}} +… \\ $$$$\therefore{f}\left({x}^{{t}} \right)=\underset{{n}=\mathrm{0}} {\overset{{k}} {\sum}}{x}^{{t}+{n}} {a}_{{n}} ={x}^{{t}−\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{{k}} {\sum}}{x}^{{n}+\mathrm{1}} {a}_{{n}} \\ $$$$ \\ $$$$\therefore{f}\left({x}^{\mathrm{3}} \right)={x}^{\mathrm{3}} \left({a}_{\mathrm{0}} +{xa}_{\mathrm{1}} +…\right)={x}^{\mathrm{2}} {f}\left({x}\right) \\ $$$${f}\left({x}^{\mathrm{3}} \right)={x}^{\mathrm{2}} {f}\left({x}\right) \\ $$$$\therefore\sqrt{{f}\left({x}^{\mathrm{3}} \right)}={x}\sqrt{{f}\left({x}\right)} \\ $$
Commented by Tawakalitu. last updated on 14/Sep/16
$${I}\:{really}\:{appreciate}\:{sir}.\:{thank}\:{you}. \\ $$
Commented by Rasheed Soomro last updated on 14/Sep/16
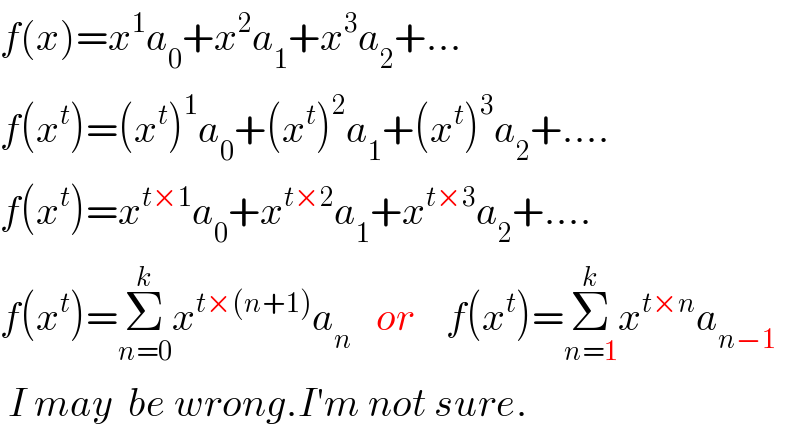
$${f}\left({x}\right)={x}^{\mathrm{1}} {a}_{\mathrm{0}} +{x}^{\mathrm{2}} {a}_{\mathrm{1}} +{x}^{\mathrm{3}} {a}_{\mathrm{2}} +… \\ $$$${f}\left({x}^{{t}} \right)=\left({x}^{{t}} \right)^{\mathrm{1}} {a}_{\mathrm{0}} +\left({x}^{{t}} \right)^{\mathrm{2}} {a}_{\mathrm{1}} +\left({x}^{{t}} \right)^{\mathrm{3}} {a}_{\mathrm{2}} +…. \\ $$$${f}\left({x}^{{t}} \right)={x}^{{t}×\mathrm{1}} {a}_{\mathrm{0}} +{x}^{{t}×\mathrm{2}} {a}_{\mathrm{1}} +{x}^{{t}×\mathrm{3}} {a}_{\mathrm{2}} +…. \\ $$$${f}\left({x}^{{t}} \right)=\underset{{n}=\mathrm{0}} {\overset{{k}} {\sum}}{x}^{{t}×\left({n}+\mathrm{1}\right)} {a}_{{n}} \:\:\:{or}\:\:\:\:{f}\left({x}^{{t}} \right)=\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}{x}^{{t}×{n}} {a}_{{n}−\mathrm{1}} \\ $$$$\:{I}\:{may}\:\:{be}\:{wrong}.{I}'{m}\:{not}\:{sure}. \\ $$
Commented by ajaenuri86@gmail.com last updated on 14/Sep/16

$${true} \\ $$
Commented by Tawakalitu. last updated on 14/Sep/16
$${Thanks}\:{for}\:{your}\:{contribution}\:{sir}. \\ $$
Commented by Rasheed Soomro last updated on 15/Sep/16
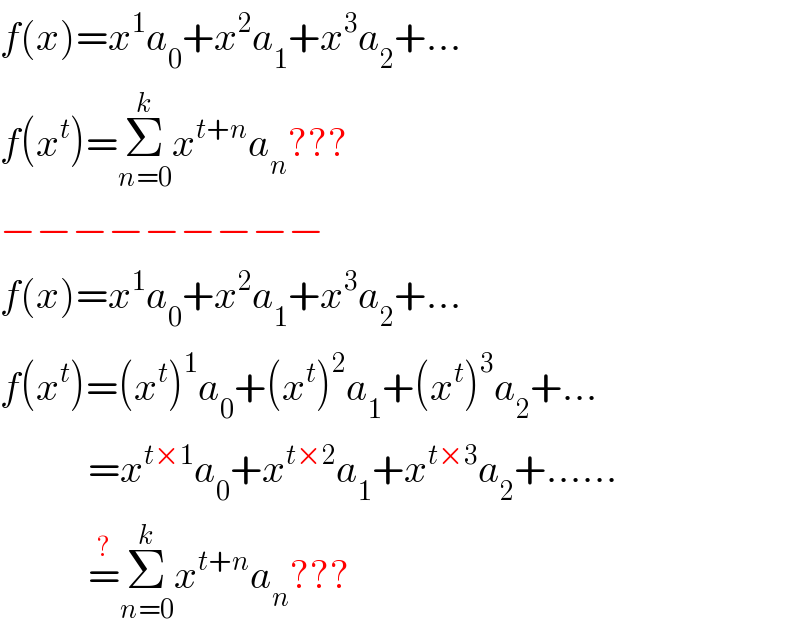
$${f}\left({x}\right)={x}^{\mathrm{1}} {a}_{\mathrm{0}} +{x}^{\mathrm{2}} {a}_{\mathrm{1}} +{x}^{\mathrm{3}} {a}_{\mathrm{2}} +… \\ $$$${f}\left({x}^{{t}} \right)=\underset{{n}=\mathrm{0}} {\overset{{k}} {\sum}}{x}^{{t}+{n}} {a}_{{n}} ??? \\ $$$$−−−−−−−−− \\ $$$${f}\left({x}\right)={x}^{\mathrm{1}} {a}_{\mathrm{0}} +{x}^{\mathrm{2}} {a}_{\mathrm{1}} +{x}^{\mathrm{3}} {a}_{\mathrm{2}} +… \\ $$$${f}\left({x}^{{t}} \right)=\left({x}^{{t}} \right)^{\mathrm{1}} {a}_{\mathrm{0}} +\left({x}^{{t}} \right)^{\mathrm{2}} {a}_{\mathrm{1}} +\left({x}^{{t}} \right)^{\mathrm{3}} {a}_{\mathrm{2}} +… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={x}^{{t}×\mathrm{1}} {a}_{\mathrm{0}} +{x}^{{t}×\mathrm{2}} {a}_{\mathrm{1}} +{x}^{{t}×\mathrm{3}} {a}_{\mathrm{2}} +…… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\overset{?} {=}\underset{{n}=\mathrm{0}} {\overset{{k}} {\sum}}{x}^{{t}+{n}} {a}_{{n}} ??? \\ $$
