Question-73346

Question Number 73346 by TawaTawa last updated on 10/Nov/19

Commented by mathmax by abdo last updated on 10/Nov/19

a) Σ_(k=0) ^n (2+3k)^2 =4+Σ_(k=1) ^n (4+12k +9k^2 ) =4 +4n +12Σ_(k=1) ^n k +9 Σ_(k=1) ^n k^2 =4n+4 +12((n(n+1))/2) +9 ((n(n+1)(2n+1))/6) =4n+4 +6n(n+1) +(3/2)n(n+1)(2n+1).

$$\left.{a}\right)\:\sum_{{k}=\mathrm{0}} ^{{n}} \left(\mathrm{2}+\mathrm{3}{k}\right)^{\mathrm{2}} \:=\mathrm{4}+\sum_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{4}+\mathrm{12}{k}\:+\mathrm{9}{k}^{\mathrm{2}} \right) \\ $$$$=\mathrm{4}\:+\mathrm{4}{n}\:+\mathrm{12}\sum_{{k}=\mathrm{1}} ^{{n}} {k}\:+\mathrm{9}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{2}} \\ $$$$=\mathrm{4}{n}+\mathrm{4}\:+\mathrm{12}\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:+\mathrm{9}\:\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$$=\mathrm{4}{n}+\mathrm{4}\:+\mathrm{6}{n}\left({n}+\mathrm{1}\right)\:+\frac{\mathrm{3}}{\mathrm{2}}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right). \\ $$

Commented by mathmax by abdo last updated on 10/Nov/19

b) Σ_(k=0) ^n C_n ^k 3^k =Σ_(k=0) ^n C_n ^k 3^k ×1^(n−k) =(3+1)^n =4^n

$$\left.{b}\right)\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\mathrm{3}^{{k}} \:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\mathrm{3}^{{k}} ×\mathrm{1}^{{n}−{k}} \:=\left(\mathrm{3}+\mathrm{1}\right)^{{n}} =\mathrm{4}^{{n}} \\ $$

Commented by mathmax by abdo last updated on 10/Nov/19

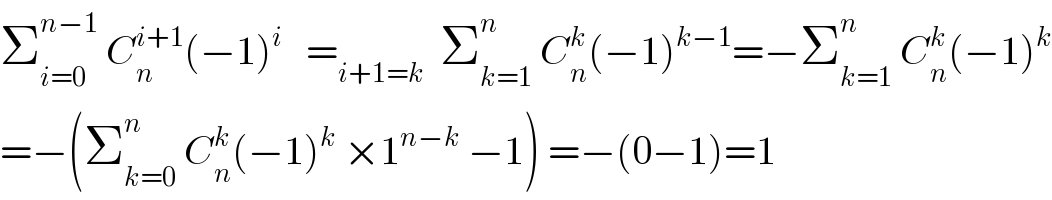
Σ_(i=0) ^(n−1) C_n ^(i+1) (−1)^i =_(i+1=k) Σ_(k=1) ^n C_n ^k (−1)^(k−1) =−Σ_(k=1) ^n C_n ^k (−1)^k =−(Σ_(k=0) ^n C_n ^k (−1)^k ×1^(n−k) −1) =−(0−1)=1

$$\sum_{{i}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{C}_{{n}} ^{{i}+\mathrm{1}} \left(−\mathrm{1}\right)^{{i}} \:\:\:=_{{i}+\mathrm{1}={k}} \:\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}−\mathrm{1}} =−\sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} \\ $$$$=−\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} \:×\mathrm{1}^{{n}−{k}} \:−\mathrm{1}\right)\:=−\left(\mathrm{0}−\mathrm{1}\right)=\mathrm{1} \\ $$

Commented by TawaTawa last updated on 10/Nov/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mathmax by abdo last updated on 10/Nov/19

$${you}\:{are}\:{welcome}. \\ $$

Answered by JDamian last updated on 10/Nov/19

(b) Σ_(k=0) ^n 3^k ((n),(k) )=Σ_(k=0) ^n 3^k 1^(n−k) ((n),(k) ) =(3+1)^n =4^n

$$\left({b}\right)\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{3}^{{k}} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{3}^{{k}} \mathrm{1}^{{n}−{k}} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:=\left(\mathrm{3}+\mathrm{1}\right)^{{n}} =\mathrm{4}^{{n}} \\ $$

Commented by TawaTawa last updated on 10/Nov/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by JDamian last updated on 10/Nov/19

(a) Σ_(k=0) ^n (2+3k)^2 = =Σ_(k=0) ^n (4+12k+9k^2 )= =Σ_(k=0) ^n 4 + 12Σ_(k=0) ^n k + 9Σ_(k=0) ^n k^2 = =4(n+1)+12(((n+1)n)/2)+9((n(n+1)(2n+1))/6)=

$$\left({a}\right)\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\mathrm{2}+\mathrm{3}{k}\right)^{\mathrm{2}} = \\ $$$$\:\:\:\:\:\:\:=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\mathrm{4}+\mathrm{12}{k}+\mathrm{9}{k}^{\mathrm{2}} \right)= \\ $$$$\:\:\:\:\:\:\:=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{4}\:+\:\mathrm{12}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\:+\:\mathrm{9}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} = \\ $$$$\:\:\:\:\:\:\:=\mathrm{4}\left({n}+\mathrm{1}\right)+\mathrm{12}\frac{\left({n}+\mathrm{1}\right){n}}{\mathrm{2}}+\mathrm{9}\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}= \\ $$

Commented by TawaTawa last updated on 10/Nov/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 10/Nov/19

Σ_(i=0) ^(n−1) (−1)^i (_(i+1) ^n ) =Σ_(i=1) ^n (−1)^(k−1) (_k ^n ) =−Σ_(i=1) ^n (−1)^k (_k ^n ) =−Σ_(i=0) ^n (−1)^k (_k ^n )+1 =−(1−1)^n +1 =1

$$\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \left(_{{i}+\mathrm{1}} ^{{n}} \right) \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \left(_{{k}} ^{{n}} \right) \\ $$$$=−\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \left(_{{k}} ^{{n}} \right) \\ $$$$=−\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \left(_{{k}} ^{{n}} \right)+\mathrm{1} \\ $$$$=−\left(\mathrm{1}−\mathrm{1}\right)^{{n}} +\mathrm{1} \\ $$$$=\mathrm{1} \\ $$

Commented by TawaTawa last updated on 10/Nov/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply