Question Number 73484 by abdomathmax last updated on 13/Nov/19
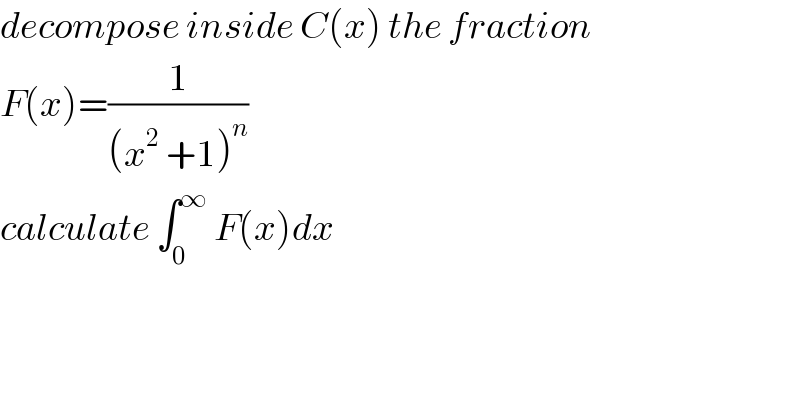
$${decompose}\:{inside}\:{C}\left({x}\right)\:{the}\:{fraction} \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{{n}} } \\ $$$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:{F}\left({x}\right){dx} \\ $$
Answered by mind is power last updated on 13/Nov/19
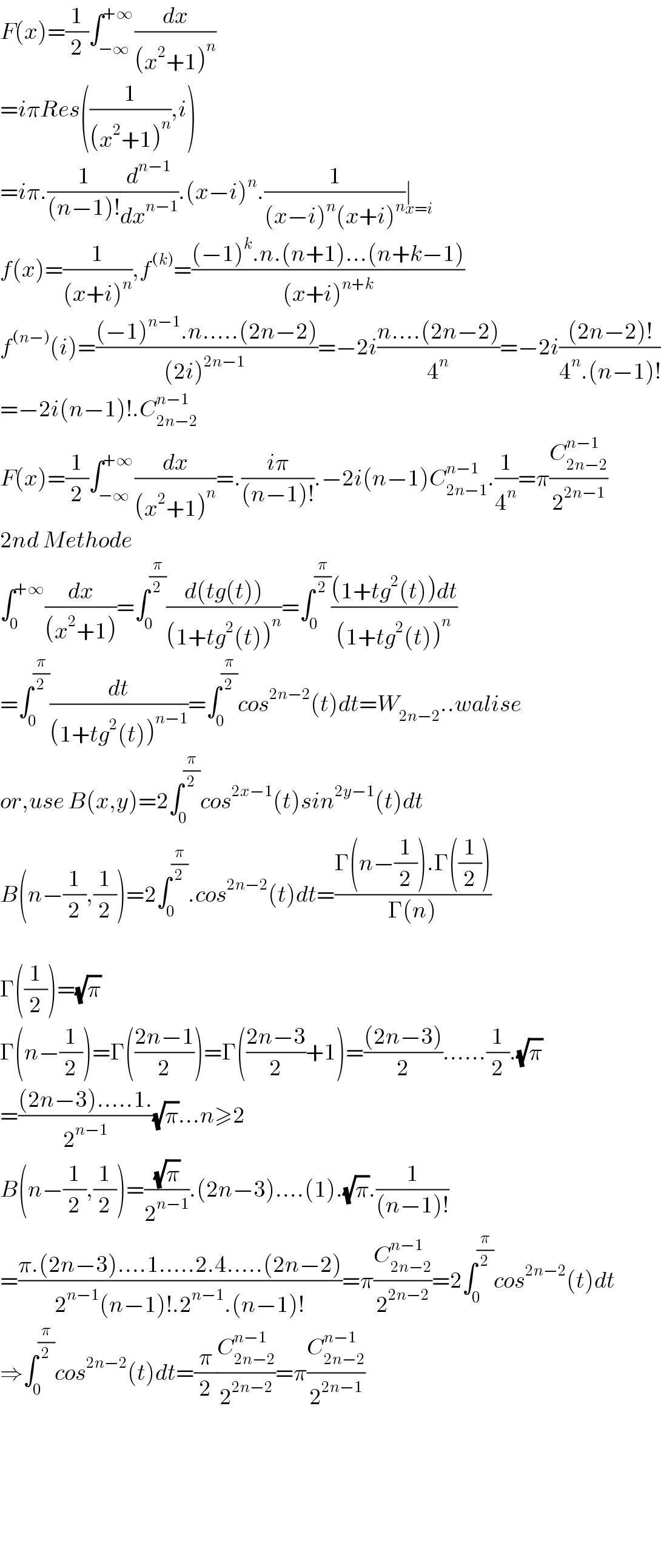
$${F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{n}} } \\ $$$$={i}\pi{Res}\left(\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{n}} },{i}\right) \\ $$$$={i}\pi.\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\frac{{d}^{{n}−\mathrm{1}} }{{dx}^{{n}−\mathrm{1}} }.\left({x}−{i}\right)^{{n}} .\frac{\mathrm{1}}{\left({x}−{i}\right)^{{n}} \left({x}+{i}\right)^{{n}} }\underset{{x}={i}} {\mid} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\left({x}+{i}\right)^{{n}} },{f}^{\left({k}\right)} =\frac{\left(−\mathrm{1}\right)^{{k}} .{n}.\left({n}+\mathrm{1}\right)…\left({n}+{k}−\mathrm{1}\right)}{\left({x}+{i}\right)^{{n}+{k}} } \\ $$$${f}^{\left({n}−\right)} \left({i}\right)=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} .{n}…..\left(\mathrm{2}{n}−\mathrm{2}\right)}{\left(\mathrm{2}{i}\right)^{\mathrm{2}{n}−\mathrm{1}} \:}=−\mathrm{2}{i}\frac{{n}….\left(\mathrm{2}{n}−\mathrm{2}\right)}{\mathrm{4}^{{n}} }=−\mathrm{2}{i}\frac{\left(\mathrm{2}{n}−\mathrm{2}\right)!}{\mathrm{4}^{{n}} .\left({n}−\mathrm{1}\right)!} \\ $$$$=−\mathrm{2}{i}\left({n}−\mathrm{1}\right)!.{C}_{\mathrm{2}{n}−\mathrm{2}} ^{{n}−\mathrm{1}} \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{n}} }=.\frac{{i}\pi}{\left({n}−\mathrm{1}\right)!}.−\mathrm{2}{i}\left({n}−\mathrm{1}\right){C}_{\mathrm{2}{n}−\mathrm{1}} ^{{n}−\mathrm{1}} .\frac{\mathrm{1}}{\mathrm{4}^{{n}} }=\pi\frac{{C}_{\mathrm{2}{n}−\mathrm{2}} ^{{n}−\mathrm{1}} }{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} } \\ $$$$\mathrm{2}{nd}\:{Methode} \\ $$$$\int_{\mathrm{0}} ^{+\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left({tg}\left({t}\right)\right)}{\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right)^{{n}} }=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right){dt}}{\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right)^{{n}} } \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dt}}{\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right)^{{n}−\mathrm{1}} }=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}{n}−\mathrm{2}} \left({t}\right){dt}={W}_{\mathrm{2}{n}−\mathrm{2}} ..{walise} \\ $$$${or},{use}\:{B}\left({x},{y}\right)=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}{x}−\mathrm{1}} \left({t}\right){sin}^{\mathrm{2}{y}−\mathrm{1}} \left({t}\right){dt} \\ $$$${B}\left({n}−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} .{cos}^{\mathrm{2}{n}−\mathrm{2}} \left({t}\right){dt}=\frac{\Gamma\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left({n}\right)} \\ $$$$ \\ $$$$\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\pi} \\ $$$$\Gamma\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\Gamma\left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\right)=\Gamma\left(\frac{\mathrm{2}{n}−\mathrm{3}}{\mathrm{2}}+\mathrm{1}\right)=\frac{\left(\mathrm{2}{n}−\mathrm{3}\right)}{\mathrm{2}}……\frac{\mathrm{1}}{\mathrm{2}}.\sqrt{\pi} \\ $$$$=\frac{\left(\mathrm{2}{n}−\mathrm{3}\right)…..\mathrm{1}.}{\mathrm{2}^{{n}−\mathrm{1}} }\sqrt{\pi}…{n}\geqslant\mathrm{2} \\ $$$${B}\left({n}−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}^{{n}−\mathrm{1}} }.\left(\mathrm{2}{n}−\mathrm{3}\right)….\left(\mathrm{1}\right).\sqrt{\pi}.\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!} \\ $$$$=\frac{\pi.\left(\mathrm{2}{n}−\mathrm{3}\right)….\mathrm{1}…..\mathrm{2}.\mathrm{4}…..\left(\mathrm{2}{n}−\mathrm{2}\right)}{\mathrm{2}^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!.\mathrm{2}^{{n}−\mathrm{1}} .\left({n}−\mathrm{1}\right)!}=\pi\frac{{C}_{\mathrm{2}{n}−\mathrm{2}} ^{{n}−\mathrm{1}} }{\mathrm{2}^{\mathrm{2}{n}−\mathrm{2}} }=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}{n}−\mathrm{2}} \left({t}\right){dt} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}{n}−\mathrm{2}} \left({t}\right){dt}=\frac{\pi}{\mathrm{2}}\frac{{C}_{\mathrm{2}{n}−\mathrm{2}} ^{{n}−\mathrm{1}} }{\mathrm{2}^{\mathrm{2}{n}−\mathrm{2}} }=\pi\frac{{C}_{\mathrm{2}{n}−\mathrm{2}} ^{{n}−\mathrm{1}} }{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} } \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by abdomathmax last updated on 17/Nov/19

$${thsnkx}\:{sir}. \\ $$
Commented by mind is power last updated on 17/Nov/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$
