Question Number 139024 by bramlexs22 last updated on 21/Apr/21
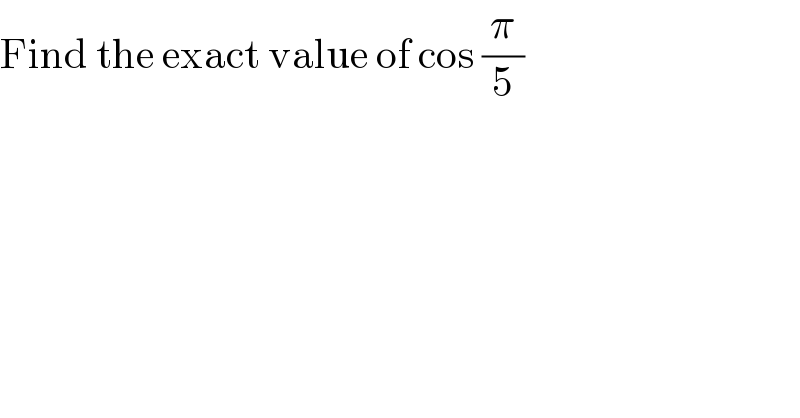
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{value}\:\mathrm{of}\:\mathrm{cos}\:\frac{\pi}{\mathrm{5}} \\ $$$$ \\ $$
Commented by EDWIN88 last updated on 21/Apr/21

$$\:\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}} \\ $$
Answered by Dwaipayan Shikari last updated on 21/Apr/21
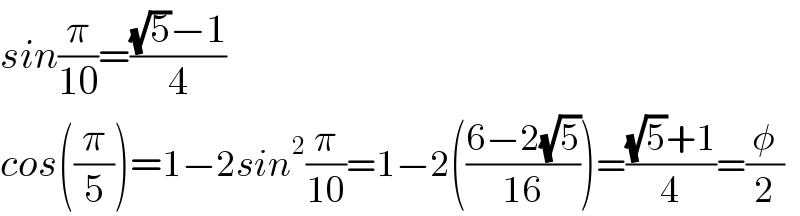
$${sin}\frac{\pi}{\mathrm{10}}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\:\:\: \\ $$$${cos}\left(\frac{\pi}{\mathrm{5}}\right)=\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{10}}=\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\right)=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}}=\frac{\phi}{\mathrm{2}} \\ $$
Answered by MJS_new last updated on 21/Apr/21
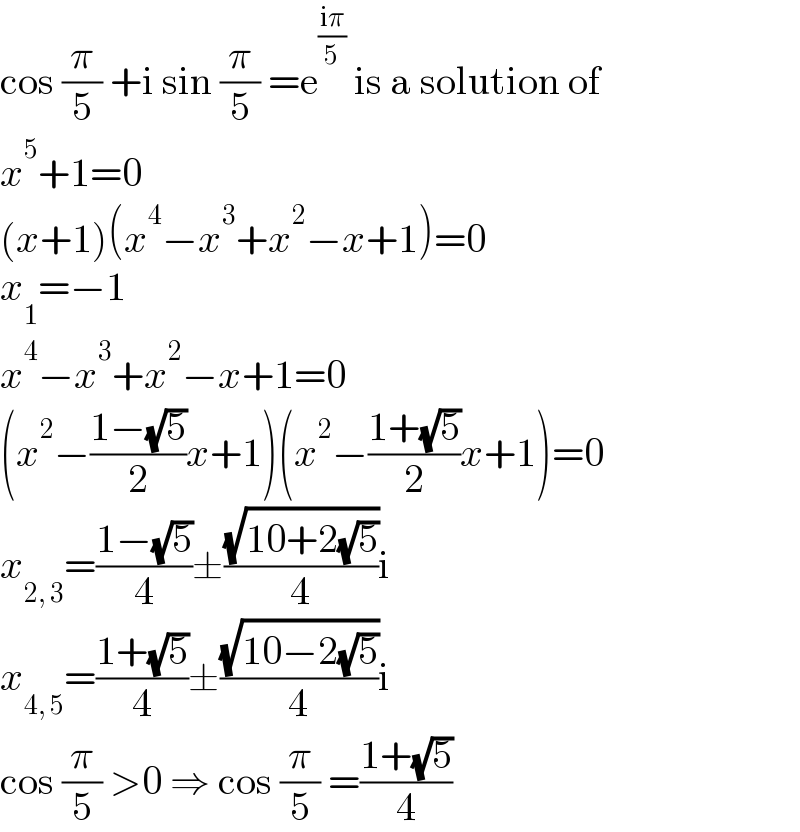
$$\mathrm{cos}\:\frac{\pi}{\mathrm{5}}\:+\mathrm{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{5}}\:=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{5}}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{of} \\ $$$${x}^{\mathrm{5}} +\mathrm{1}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =−\mathrm{1} \\ $$$${x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{2},\:\mathrm{3}} =\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}\pm\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}\mathrm{i} \\ $$$${x}_{\mathrm{4},\:\mathrm{5}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\pm\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}\mathrm{i} \\ $$$$\mathrm{cos}\:\frac{\pi}{\mathrm{5}}\:>\mathrm{0}\:\Rightarrow\:\mathrm{cos}\:\frac{\pi}{\mathrm{5}}\:=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$
