Menu Close

Given-f-x-1-x-2-x-x-1-find-f-x-

Tinku Tara 0 Comments
Pin




Question Number 139029 by bramlexs22 last updated on 21/Apr/21
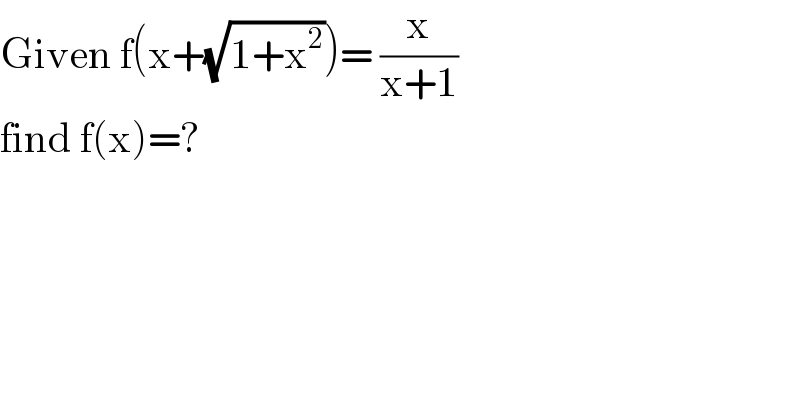
Given f(x+(√(1+x^2 )))= (x/(x+1)) find f(x)=?
$$\mathrm{Given}\:\mathrm{f}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)=\:\frac{\mathrm{x}}{\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{find}\:\mathrm{f}\left(\mathrm{x}\right)=? \\ $$
Answered by EDWIN88 last updated on 21/Apr/21
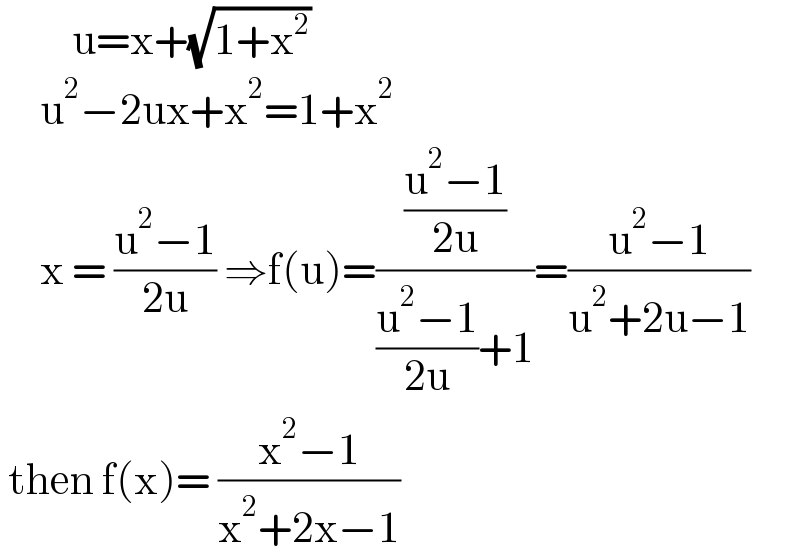
u=x+(√(1+x^2 )) u^2 −2ux+x^2 =1+x^2 x = ((u^2 −1)/(2u)) ⇒f(u)=(((u^2 −1)/(2u))/(((u^2 −1)/(2u))+1))=((u^2 −1)/(u^2 +2u−1)) then f(x)= ((x^2 −1)/(x^2 +2x−1))
$$\:\:\:\:\:\:\:\:\:\mathrm{u}=\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\mathrm{u}^{\mathrm{2}} −\mathrm{2ux}+\mathrm{x}^{\mathrm{2}} =\mathrm{1}+\mathrm{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{x}\:=\:\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2u}}\:\Rightarrow\mathrm{f}\left(\mathrm{u}\right)=\frac{\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2u}}}{\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2u}}+\mathrm{1}}=\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{u}^{\mathrm{2}} +\mathrm{2u}−\mathrm{1}} \\ $$$$\:\mathrm{then}\:\mathrm{f}\left(\mathrm{x}\right)=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{1}} \\ $$
Answered by mathmax by abdo last updated on 22/Apr/21
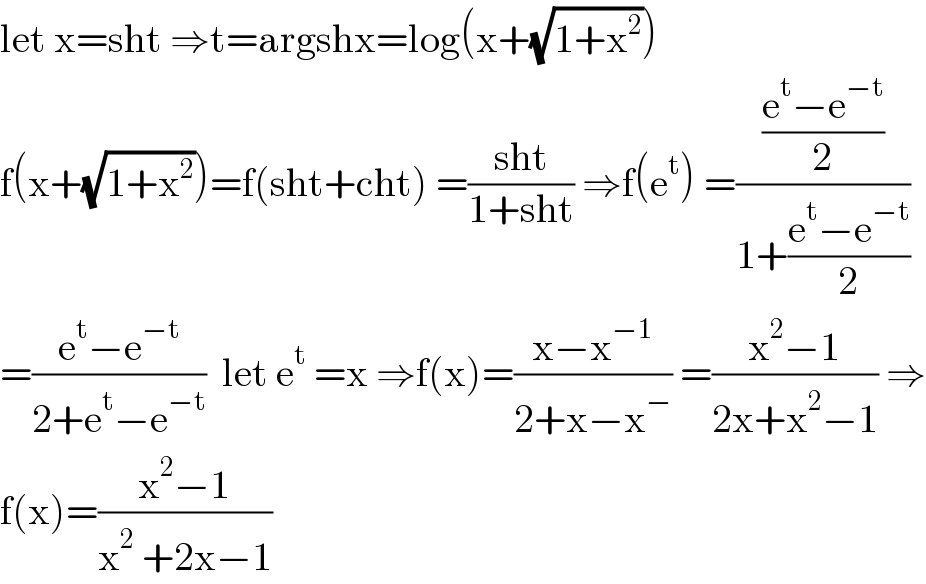
let x=sht ⇒t=argshx=log(x+(√(1+x^2 ))) f(x+(√(1+x^2 )))=f(sht+cht) =((sht)/(1+sht)) ⇒f(e^t ) =(((e^t −e^(−t) )/2)/(1+((e^t −e^(−t) )/2))) =((e^t −e^(−t) )/(2+e^t −e^(−t) )) let e^t =x ⇒f(x)=((x−x^(−1) )/(2+x−x^− )) =((x^2 −1)/(2x+x^2 −1)) ⇒ f(x)=((x^2 −1)/(x^2 +2x−1))
$$\mathrm{let}\:\mathrm{x}=\mathrm{sht}\:\Rightarrow\mathrm{t}=\mathrm{argshx}=\mathrm{log}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right) \\ $$$$\mathrm{f}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)=\mathrm{f}\left(\mathrm{sht}+\mathrm{cht}\right)\:=\frac{\mathrm{sht}}{\mathrm{1}+\mathrm{sht}}\:\Rightarrow\mathrm{f}\left(\mathrm{e}^{\mathrm{t}} \right)\:=\frac{\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}}{\mathrm{1}+\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}} \\ $$$$=\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}+\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }\:\:\mathrm{let}\:\mathrm{e}^{\mathrm{t}} \:=\mathrm{x}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}−\mathrm{x}^{−\mathrm{1}} }{\mathrm{2}+\mathrm{x}−\mathrm{x}^{−} }\:=\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2x}+\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}−\mathrm{1}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *