Question Number 73567 by Rio Michael last updated on 13/Nov/19
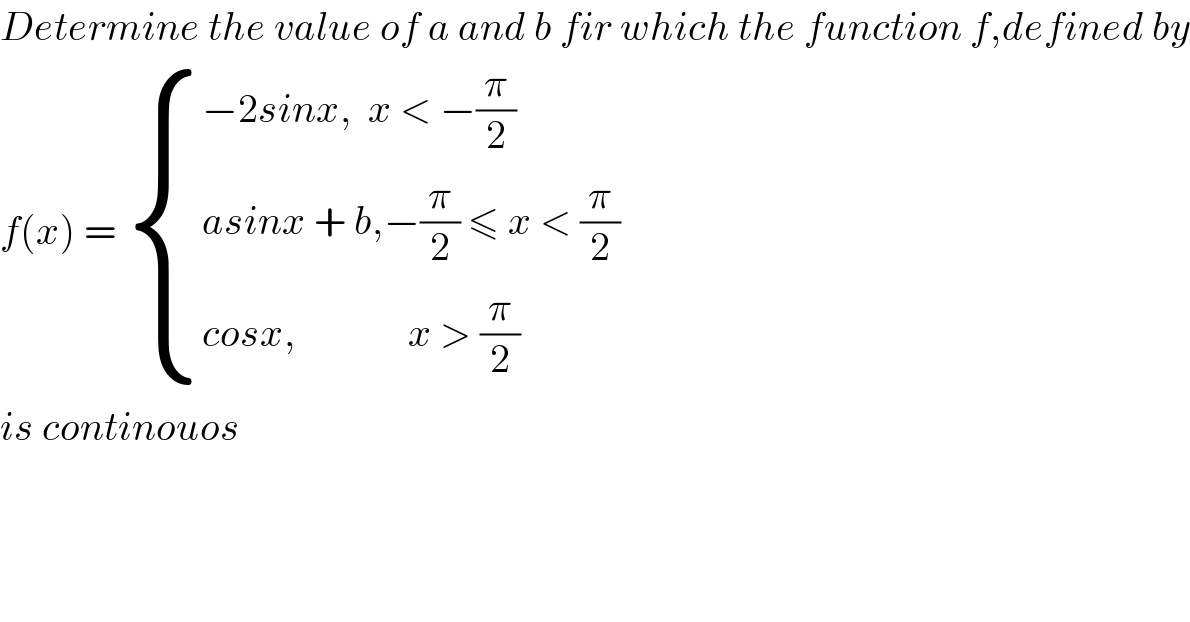
$${Determine}\:{the}\:{value}\:{of}\:{a}\:{and}\:{b}\:{fir}\:{which}\:{the}\:{function}\:{f},{defined}\:{by} \\ $$$${f}\left({x}\right)\:=\:\begin{cases}{−\mathrm{2}{sinx},\:\:{x}\:<\:−\frac{\pi}{\mathrm{2}}}\\{{asinx}\:+\:{b},−\frac{\pi}{\mathrm{2}}\:\leqslant\:{x}\:<\:\frac{\pi}{\mathrm{2}}}\\{{cosx},\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:>\:\frac{\pi}{\mathrm{2}}}\end{cases} \\ $$$${is}\:{continouos} \\ $$
Commented by Rio Michael last updated on 13/Nov/19

$${thank}\:{you} \\ $$
Commented by kaivan.ahmadi last updated on 13/Nov/19
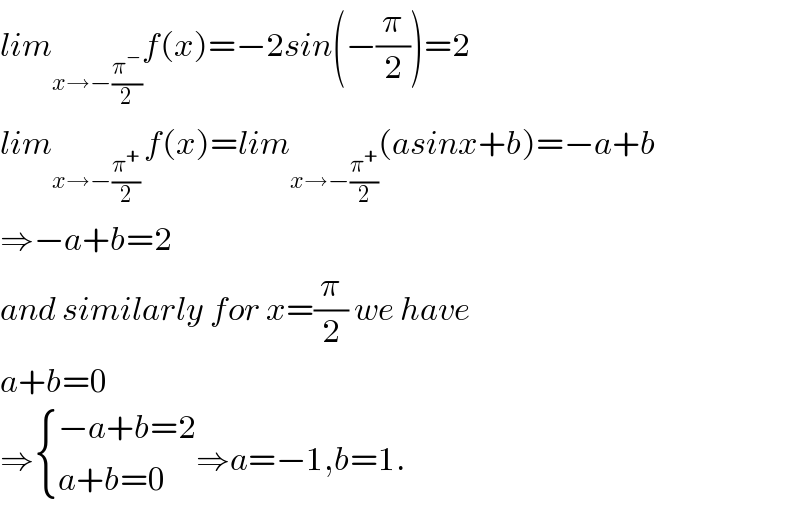
$${lim}_{{x}\rightarrow−\frac{\pi^{−} }{\mathrm{2}}} {f}\left({x}\right)=−\mathrm{2}{sin}\left(−\frac{\pi}{\mathrm{2}}\right)=\mathrm{2} \\ $$$${lim}_{{x}\rightarrow−\frac{\pi^{+} }{\mathrm{2}}\:} {f}\left({x}\right)={lim}_{{x}\rightarrow−\frac{\pi^{+} }{\mathrm{2}}} \left({asinx}+{b}\right)=−{a}+{b} \\ $$$$\Rightarrow−{a}+{b}=\mathrm{2} \\ $$$${and}\:{similarly}\:{for}\:{x}=\frac{\pi}{\mathrm{2}}\:{we}\:{have} \\ $$$${a}+{b}=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{−{a}+{b}=\mathrm{2}}\\{{a}+{b}=\mathrm{0}}\end{cases}\Rightarrow{a}=−\mathrm{1},{b}=\mathrm{1}. \\ $$
