Question Number 139153 by henderson last updated on 23/Apr/21
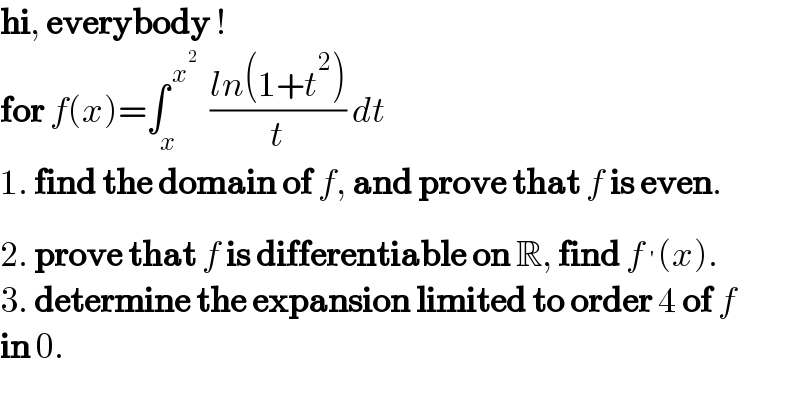
$$\boldsymbol{\mathrm{hi}},\:\boldsymbol{\mathrm{everybody}}\:! \\ $$$$\boldsymbol{\mathrm{for}}\:{f}\left({x}\right)=\int_{{x}} ^{\:{x}^{\mathrm{2}} } \:\:\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{{t}}\:{dt} \\ $$$$\mathrm{1}.\:\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{domain}}\:\boldsymbol{\mathrm{of}}\:{f},\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}\:{f}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{even}}. \\ $$$$\mathrm{2}.\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}\:{f}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{differentiable}}\:\boldsymbol{\mathrm{on}}\:\mathbb{R},\:\boldsymbol{\mathrm{find}}\:{f}\:^{'} \left({x}\right). \\ $$$$\mathrm{3}.\:\boldsymbol{\mathrm{determine}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{expansion}}\:\boldsymbol{\mathrm{limited}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{order}}\:\mathrm{4}\:\boldsymbol{\mathrm{of}}\:{f} \\ $$$$\boldsymbol{\mathrm{in}}\:\mathrm{0}. \\ $$
Commented by greg_ed last updated on 23/Apr/21

$$\mathrm{this}\:\mathrm{thing}\:\mathrm{looks}\:\mathrm{very}\:\mathrm{interesting}\::\:\mathrm{we}\:\mathrm{shouldn}'\mathrm{t} \\ $$$$\mathrm{ignore}\:\mathrm{it},\:\mathrm{guyz}\:! \\ $$
