Question Number 139283 by qaz last updated on 25/Apr/21

$$\int_{\mathrm{0}} ^{\infty} \frac{{ln}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{8}{a}}\left(\pi^{\mathrm{2}} +\mathrm{4}{ln}^{\mathrm{2}} {a}\right)\:\:\:\:\:\:\:\:\:,{a}>\mathrm{0} \\ $$
Answered by Ar Brandon last updated on 10/Aug/21
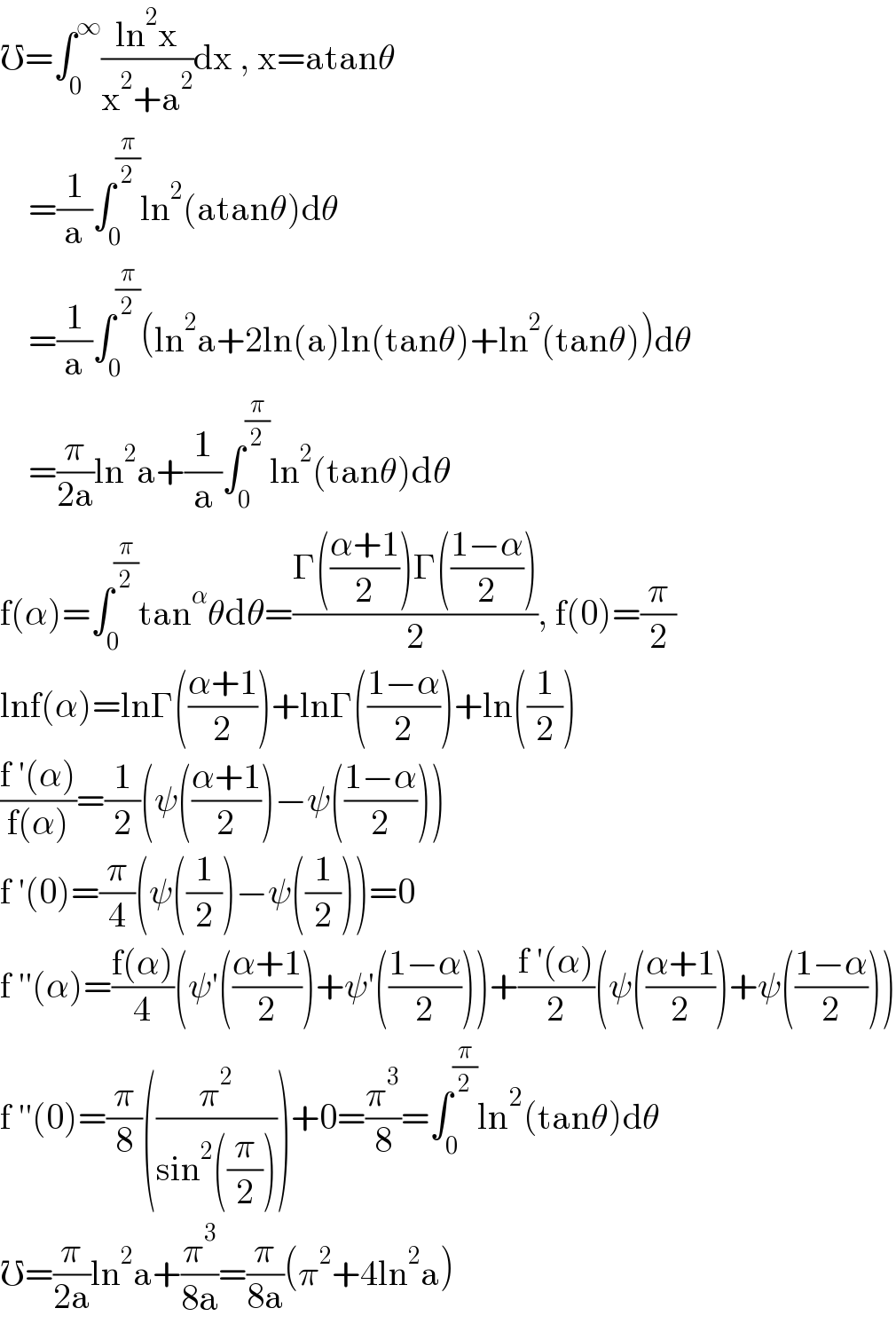
$$\mho=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\:,\:\mathrm{x}=\mathrm{atan}\theta \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{atan}\theta\right)\mathrm{d}\theta \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{ln}^{\mathrm{2}} \mathrm{a}+\mathrm{2ln}\left(\mathrm{a}\right)\mathrm{ln}\left(\mathrm{tan}\theta\right)+\mathrm{ln}^{\mathrm{2}} \left(\mathrm{tan}\theta\right)\right)\mathrm{d}\theta \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{2a}}\mathrm{ln}^{\mathrm{2}} \mathrm{a}+\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{tan}\theta\right)\mathrm{d}\theta \\ $$$$\mathrm{f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{tan}^{\alpha} \theta\mathrm{d}\theta=\frac{\Gamma\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}−\alpha}{\mathrm{2}}\right)}{\mathrm{2}},\:\mathrm{f}\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{lnf}\left(\alpha\right)=\mathrm{ln}\Gamma\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)+\mathrm{ln}\Gamma\left(\frac{\mathrm{1}−\alpha}{\mathrm{2}}\right)+\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{f}\:'\left(\alpha\right)}{\mathrm{f}\left(\alpha\right)}=\frac{\mathrm{1}}{\mathrm{2}}\left(\psi\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{1}−\alpha}{\mathrm{2}}\right)\right) \\ $$$$\mathrm{f}\:'\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{4}}\left(\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)=\mathrm{0} \\ $$$$\mathrm{f}\:''\left(\alpha\right)=\frac{\mathrm{f}\left(\alpha\right)}{\mathrm{4}}\left(\psi'\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)+\psi'\left(\frac{\mathrm{1}−\alpha}{\mathrm{2}}\right)\right)+\frac{\mathrm{f}\:'\left(\alpha\right)}{\mathrm{2}}\left(\psi\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)+\psi\left(\frac{\mathrm{1}−\alpha}{\mathrm{2}}\right)\right) \\ $$$$\mathrm{f}\:''\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{8}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}\right)}\right)+\mathrm{0}=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{tan}\theta\right)\mathrm{d}\theta \\ $$$$\mho=\frac{\pi}{\mathrm{2a}}\mathrm{ln}^{\mathrm{2}} \mathrm{a}+\frac{\pi^{\mathrm{3}} }{\mathrm{8a}}=\frac{\pi}{\mathrm{8a}}\left(\pi^{\mathrm{2}} +\mathrm{4ln}^{\mathrm{2}} \mathrm{a}\right) \\ $$
Commented by qaz last updated on 25/Apr/21
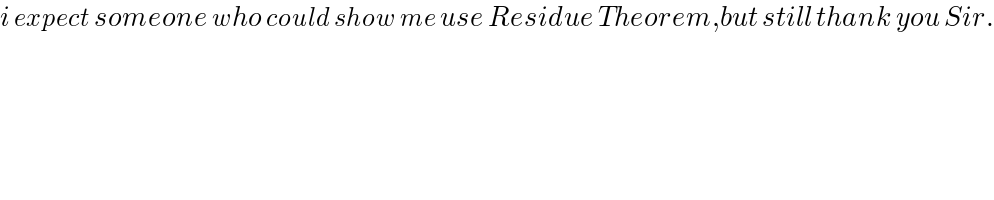
$${i}\:{expect}\:{someone}\:{who}\:{could}\:{show}\:{me}\:{use}\:{Residue}\:{Theorem},{but}\:{still}\:{thank}\:{you}\:{Sir}. \\ $$
Commented by Ar Brandon last updated on 25/Apr/21
$$\mathrm{You}'\mathrm{re}\:\mathrm{welcome},\:\mathrm{Sir} \\ $$
Answered by mathmax by abdo last updated on 26/Apr/21

$$\mathrm{f}\left(\mathrm{t}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{t}} \mathrm{lnx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{f}\left(\mathrm{t}\right)=_{\mathrm{x}=\mathrm{ay}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left(\mathrm{ay}\right)^{\mathrm{t}} \:\mathrm{ln}\left(\mathrm{ay}\right)}{\mathrm{a}^{\mathrm{2}} \left(\mathrm{y}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{ady} \\ $$$$=\mathrm{a}^{\mathrm{t}−\mathrm{1}} \:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{y}^{\mathrm{t}} \left(\mathrm{lna}+\mathrm{lny}\right)}{\mathrm{y}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dy}\:=\mathrm{a}^{\mathrm{t}−\mathrm{1}} \mathrm{lna}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{y}^{\mathrm{t}} }{\mathrm{y}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dy}\:+\mathrm{a}^{\mathrm{t}−\mathrm{1}} \int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{y}^{\mathrm{t}} }{\mathrm{y}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{lny}\:\mathrm{dy} \\ $$$$\mathrm{we}\:\mathrm{have}\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{y}^{\mathrm{t}} }{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\mathrm{dy}\:=_{\mathrm{y}^{\mathrm{2}} =\mathrm{u}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{u}^{\frac{\mathrm{t}}{\mathrm{2}}} }{\mathrm{u}+\mathrm{1}}\frac{\mathrm{du}}{\mathrm{2}\sqrt{\mathrm{u}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{u}^{\frac{\mathrm{t}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\mathrm{u}+\mathrm{1}}\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{sin}\left(\pi\left(\frac{\mathrm{t}+\mathrm{1}}{\mathrm{2}}\right)\right)}\:=\frac{\pi}{\mathrm{2sin}\left(\frac{\pi\mathrm{t}}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)} \\ $$$$=\frac{\pi}{\mathrm{2cos}\left(\frac{\pi\mathrm{t}}{\mathrm{2}}\right)}\:\mathrm{let}\:\mathrm{find}\:\Phi\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{y}^{\mathrm{t}} }{\mathrm{y}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{lny}\:\mathrm{dy} \\ $$$$\Phi=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\Sigma\:\mathrm{Res}\left(\mathrm{w}\:\mathrm{z}_{\mathrm{i}} \right)\right)\:\:\mathrm{with}\:\mathrm{w}\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{t}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{ln}^{\mathrm{2}} \mathrm{z}=\frac{\mathrm{z}^{\mathrm{t}} \mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)} \\ $$$$\mathrm{Res}\left(\mathrm{w},\mathrm{i}\right)\:=\frac{\mathrm{i}^{\mathrm{t}} \:\mathrm{ln}^{\mathrm{2}} \left(\mathrm{i}\right)}{\mathrm{2i}}\:=\frac{\mathrm{e}^{\frac{\mathrm{i}\pi\mathrm{t}}{\mathrm{2}}} \:\left(\frac{\mathrm{i}\pi}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2i}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{8i}}\:\mathrm{e}^{\frac{\mathrm{i}\pi\mathrm{t}}{\mathrm{2}}} \:=\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{8}}\:\mathrm{e}^{\frac{\mathrm{i}\pi\mathrm{t}}{\mathrm{2}}} \\ $$$$\mathrm{Res}\left(\mathrm{w},−\mathrm{i}\right)\:=−\frac{\mathrm{1}}{\mathrm{2i}}\left(−\mathrm{i}\right)^{\mathrm{t}} \:\mathrm{ln}^{\mathrm{2}} \left(−\mathrm{i}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2i}}\mathrm{e}^{−\frac{\mathrm{i}\pi\mathrm{t}}{\mathrm{2}}} \left(−\frac{\mathrm{i}\pi}{\mathrm{2}}\right)^{\mathrm{2}} \:=\frac{\pi^{\mathrm{2}} }{\mathrm{4i}}\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}} \:=−\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{8}}\mathrm{e}^{−\frac{\mathrm{i}\pi\mathrm{t}}{\mathrm{2}}} \:\Rightarrow \\ $$$$\Sigma\:\mathrm{Res}=\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{8}}\left(\mathrm{e}^{\frac{\mathrm{i}\pi\mathrm{t}}{\mathrm{2}}} −\mathrm{e}^{−\frac{\mathrm{i}\pi\mathrm{t}}{\mathrm{2}}} \right)\:=\frac{\mathrm{i}\pi^{\mathrm{2}} }{\mathrm{8}}\left(\mathrm{2i}\:\mathrm{sin}\left(\frac{\pi\mathrm{t}}{\mathrm{2}}\right)\right) \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\mathrm{sin}\left(\frac{\pi\mathrm{t}}{\mathrm{2}}\right)\:\Rightarrow\mathrm{f}\left(\mathrm{t}\right)=\mathrm{a}^{\mathrm{t}−\mathrm{1}} \mathrm{lna}.\frac{\pi}{\mathrm{2cos}\left(\frac{\pi\mathrm{t}}{\mathrm{2}}\right)} \\ $$$$−\mathrm{a}^{\mathrm{t}−\mathrm{1}} \:\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\mathrm{sin}\left(\frac{\pi\mathrm{t}}{\mathrm{2}}\right)\:\:\mathrm{but}\:\mathrm{f}\left(\mathrm{t}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{\mathrm{tlogx}} \mathrm{logx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{t}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{t}} \:\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{o}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{rest}\:\mathrm{calculus}\:\mathrm{of}\:\mathrm{f}^{'} \left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{f}^{'} \left(\mathrm{o}\right)….\mathrm{be}\:\mathrm{continued}… \\ $$
