Question Number 131717 by LYKA last updated on 07/Feb/21
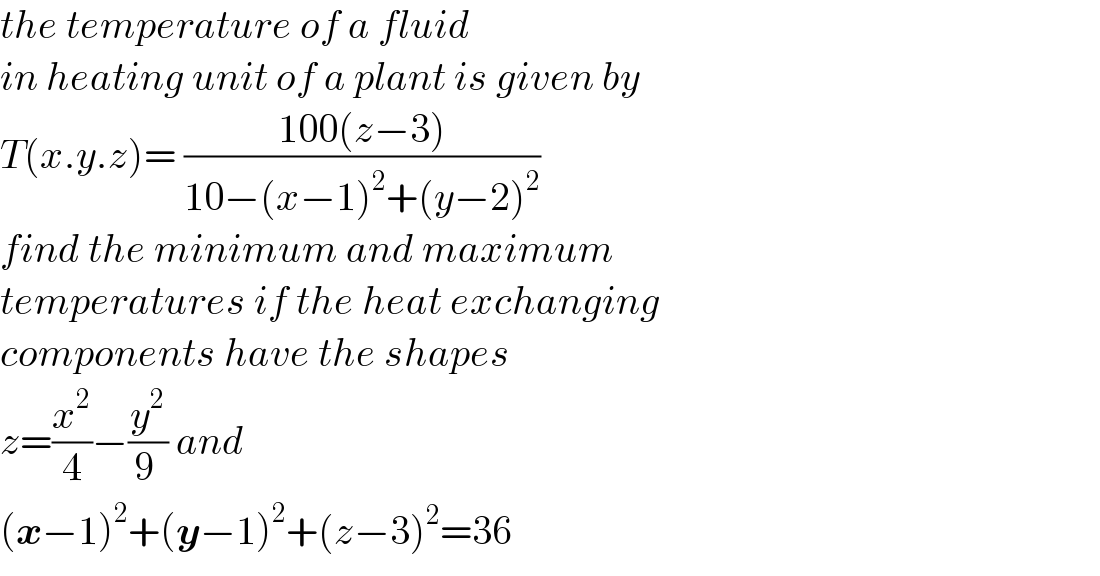
$${the}\:{temperature}\:{of}\:{a}\:{fluid} \\ $$$${in}\:{heating}\:{unit}\:{of}\:{a}\:{plant}\:{is}\:{given}\:{by} \\ $$$${T}\left({x}.{y}.{z}\right)=\:\frac{\mathrm{100}\left({z}−\mathrm{3}\right)}{\mathrm{10}−\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${find}\:{the}\:{minimum}\:{and}\:{maximum}\: \\ $$$${temperatures}\:{if}\:{the}\:{heat}\:{exchanging}\: \\ $$$${components}\:{have}\:{the}\:{shapes}\: \\ $$$${z}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{{y}^{\mathrm{2}} }{\mathrm{9}\:}\:{and}\: \\ $$$$\left(\boldsymbol{{x}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\boldsymbol{{y}}−\mathrm{1}\right)^{\mathrm{2}} +\left({z}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{36} \\ $$
