Question Number 139402 by mathmax by abdo last updated on 26/Apr/21
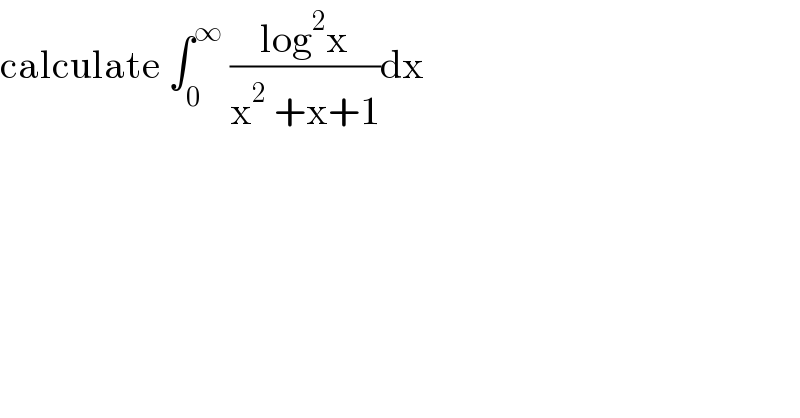
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 29/Apr/21
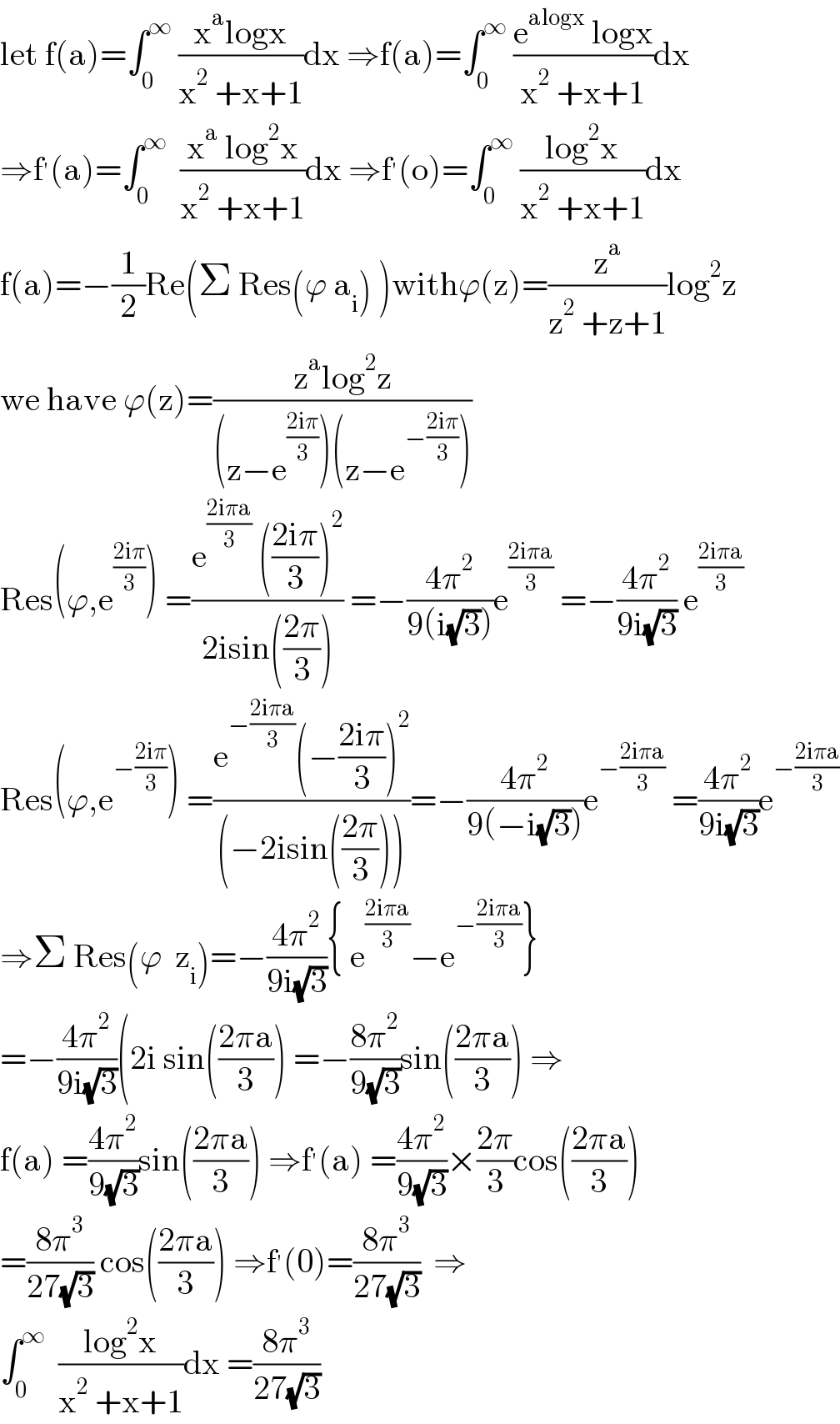
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{a}} \mathrm{logx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\mathrm{dx}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{alogx}} \:\mathrm{logx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{a}} \:\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\mathrm{dx}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{o}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\Sigma\:\mathrm{Res}\left(\varphi\:\mathrm{a}_{\mathrm{i}} \right)\:\right)\mathrm{with}\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{a}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{z}+\mathrm{1}}\mathrm{log}^{\mathrm{2}} \mathrm{z} \\ $$$$\mathrm{we}\:\mathrm{have}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{a}} \mathrm{log}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)\:=\frac{\mathrm{e}^{\frac{\mathrm{2i}\pi\mathrm{a}}{\mathrm{3}}} \:\left(\frac{\mathrm{2i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{2isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)}\:=−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{9}\left(\mathrm{i}\sqrt{\mathrm{3}}\right)}\mathrm{e}^{\frac{\mathrm{2i}\pi\mathrm{a}}{\mathrm{3}}} \:=−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{9i}\sqrt{\mathrm{3}}}\:\mathrm{e}^{\frac{\mathrm{2i}\pi\mathrm{a}}{\mathrm{3}}} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{e}^{−\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)\:=\frac{\mathrm{e}^{−\frac{\mathrm{2i}\pi\mathrm{a}}{\mathrm{3}}} \left(−\frac{\mathrm{2i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{\left(−\mathrm{2isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)}=−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{9}\left(−\mathrm{i}\sqrt{\mathrm{3}}\right)}\mathrm{e}^{−\frac{\mathrm{2i}\pi\mathrm{a}}{\mathrm{3}}} \:=\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{9i}\sqrt{\mathrm{3}}}\mathrm{e}^{−\frac{\mathrm{2i}\pi\mathrm{a}}{\mathrm{3}}} \\ $$$$\Rightarrow\Sigma\:\mathrm{Res}\left(\varphi\:\:\mathrm{z}_{\mathrm{i}} \right)=−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{9i}\sqrt{\mathrm{3}}}\left\{\:\mathrm{e}^{\frac{\mathrm{2i}\pi\mathrm{a}}{\mathrm{3}}} −\mathrm{e}^{−\frac{\mathrm{2i}\pi\mathrm{a}}{\mathrm{3}}} \right\} \\ $$$$=−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{9i}\sqrt{\mathrm{3}}}\left(\mathrm{2i}\:\mathrm{sin}\left(\frac{\mathrm{2}\pi\mathrm{a}}{\mathrm{3}}\right)\:=−\frac{\mathrm{8}\pi^{\mathrm{2}} }{\mathrm{9}\sqrt{\mathrm{3}}}\mathrm{sin}\left(\frac{\mathrm{2}\pi\mathrm{a}}{\mathrm{3}}\right)\:\Rightarrow\right. \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{9}\sqrt{\mathrm{3}}}\mathrm{sin}\left(\frac{\mathrm{2}\pi\mathrm{a}}{\mathrm{3}}\right)\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{9}\sqrt{\mathrm{3}}}×\frac{\mathrm{2}\pi}{\mathrm{3}}\mathrm{cos}\left(\frac{\mathrm{2}\pi\mathrm{a}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{8}\pi^{\mathrm{3}} }{\mathrm{27}\sqrt{\mathrm{3}}}\:\mathrm{cos}\left(\frac{\mathrm{2}\pi\mathrm{a}}{\mathrm{3}}\right)\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{0}\right)=\frac{\mathrm{8}\pi^{\mathrm{3}} }{\mathrm{27}\sqrt{\mathrm{3}}}\:\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{8}\pi^{\mathrm{3}} }{\mathrm{27}\sqrt{\mathrm{3}}} \\ $$
