Question Number 66197 by Rasheed.Sindhi last updated on 11/Aug/19
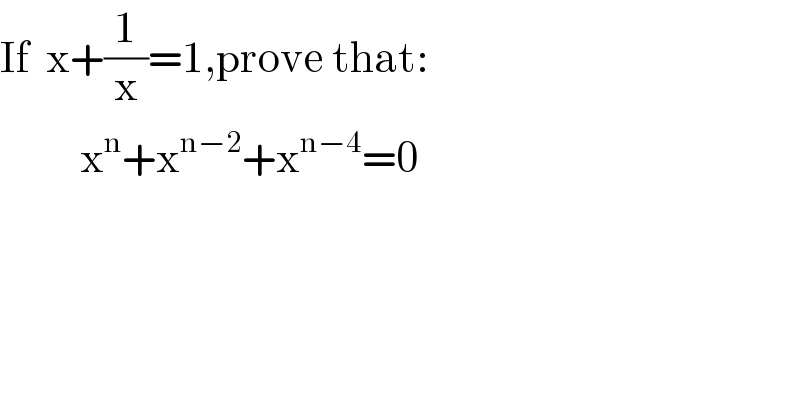
$$\mathrm{If}\:\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{1},\mathrm{prove}\:\mathrm{that}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{n}} +\mathrm{x}^{\mathrm{n}−\mathrm{2}} +\mathrm{x}^{\mathrm{n}−\mathrm{4}} =\mathrm{0} \\ $$
Commented by mr W last updated on 10/Aug/19

$$\mathcal{VERY}\:\mathcal{NICE}! \\ $$
Commented by Rasheed.Sindhi last updated on 11/Aug/19
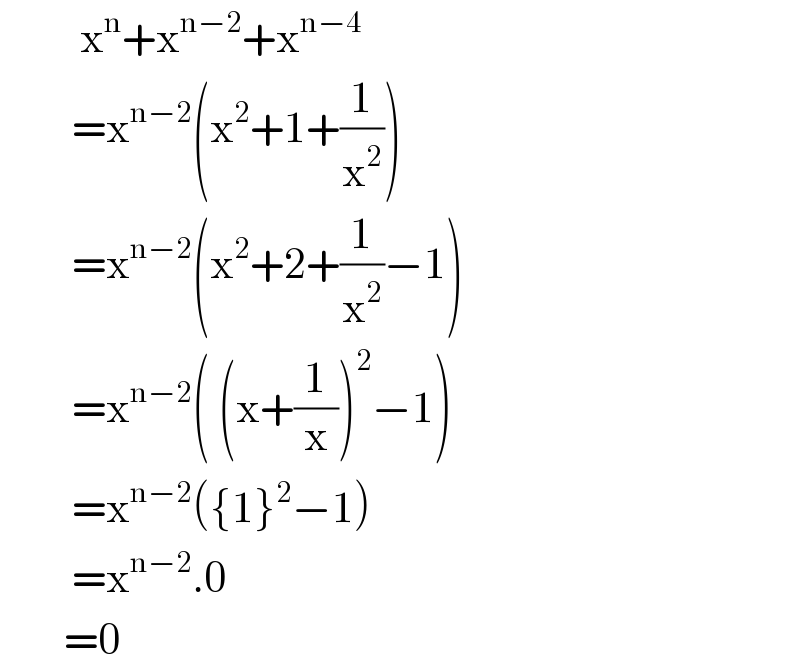
$$\:\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{n}} +\mathrm{x}^{\mathrm{n}−\mathrm{2}} +\mathrm{x}^{\mathrm{n}−\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{n}−\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{n}−\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{n}−\mathrm{2}} \left(\:\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{n}−\mathrm{2}} \left(\left\{\mathrm{1}\right\}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{n}−\mathrm{2}} .\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{0} \\ $$
Commented by Rasheed.Sindhi last updated on 11/Aug/19
$$\mathcal{T}{hank}\mathcal{S}{s}\:{for}\:\mathcal{E}{ncouraging}\:\mathcal{S}{ir}! \\ $$
Answered by som(math1967) last updated on 10/Aug/19

$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} −{x}+\mathrm{1}=\mathrm{0}\Rightarrow\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{3}} +\mathrm{1}=\mathrm{0}\therefore{x}^{\mathrm{3}} =−\mathrm{1}\:\Rightarrow{x}^{\mathrm{3}} .{x}=−{x} \\ $$$$\therefore{x}^{\mathrm{4}} =−{x} \\ $$$${Now}\:{x}^{{n}} +{x}^{{n}−\mathrm{2}} +{x}^{{n}−\mathrm{4}} \\ $$$$={x}^{{n}} \left(\mathrm{1}+{x}^{−\mathrm{2}} +{x}^{−\mathrm{4}} \right) \\ $$$$={x}^{{n}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)={x}^{{n}} \left(\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{4}} }\right) \\ $$$$={x}^{{n}} \left(\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{{x}^{\mathrm{4}} }\right)\:\:\bigstar \\ $$$$={x}^{{n}} \left(\frac{\mathrm{0}}{{x}^{\mathrm{4}} }\right)=\mathrm{0}\:\:\bigstar\left[\bigstar\right. \\ $$$$\bigstar{x}^{\mathrm{4}} =−{x}\:\:\:\:\:\: \\ $$$$\bigstar\bigstar{x}^{\mathrm{2}} −{x}+\mathrm{1}=\mathrm{0} \\ $$
Commented by Rasheed.Sindhi last updated on 11/Aug/19

$$\mathcal{TH}{anks}\:\mathcal{S}{ir}! \\ $$
Answered by mr W last updated on 10/Aug/19

$${x}\neq\mathrm{0} \\ $$$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} ={x}−\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{4}} =\left({x}−\mathrm{1}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{2}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right) \\ $$$$\Rightarrow{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}^{{n}−\mathrm{4}} \left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}^{{n}} +{x}^{{n}−\mathrm{2}} +{x}^{{n}−\mathrm{4}} =\mathrm{0} \\ $$
Commented by Rasheed.Sindhi last updated on 11/Aug/19

$$\mathbb{T}\mathrm{h}\alpha\mathrm{n}\Bbbk\mathrm{s}\:\mathrm{Sir}! \\ $$
Answered by gunawan last updated on 11/Aug/19
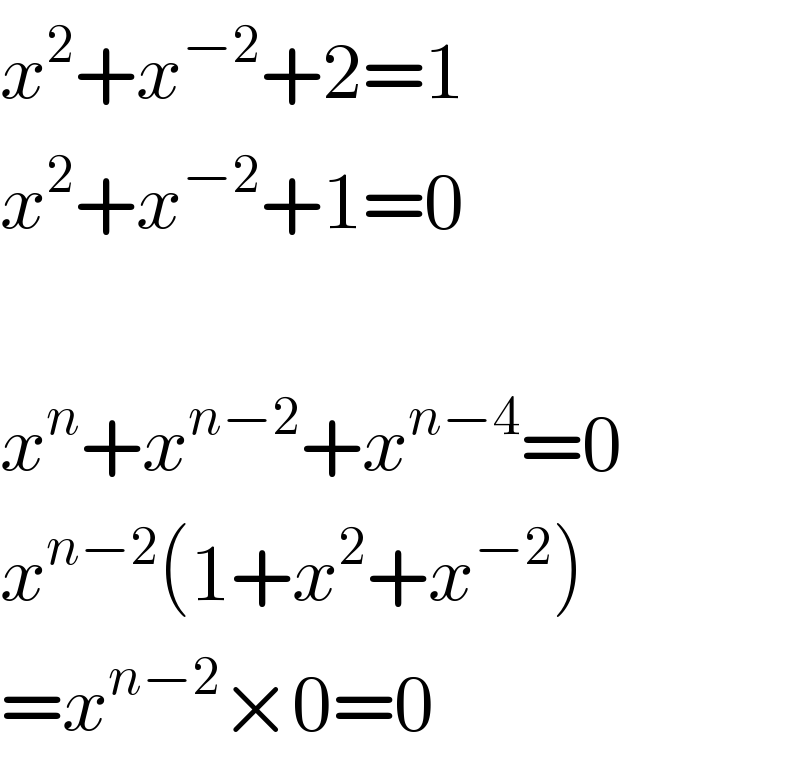
$${x}^{\mathrm{2}} +{x}^{−\mathrm{2}} +\mathrm{2}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} +{x}^{−\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$ \\ $$$${x}^{{n}} +{x}^{{n}−\mathrm{2}} +{x}^{{n}−\mathrm{4}} =\mathrm{0} \\ $$$${x}^{{n}−\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} +{x}^{−\mathrm{2}} \right) \\ $$$$={x}^{{n}−\mathrm{2}} ×\mathrm{0}=\mathrm{0} \\ $$
