Question Number 139502 by bemath last updated on 28/Apr/21
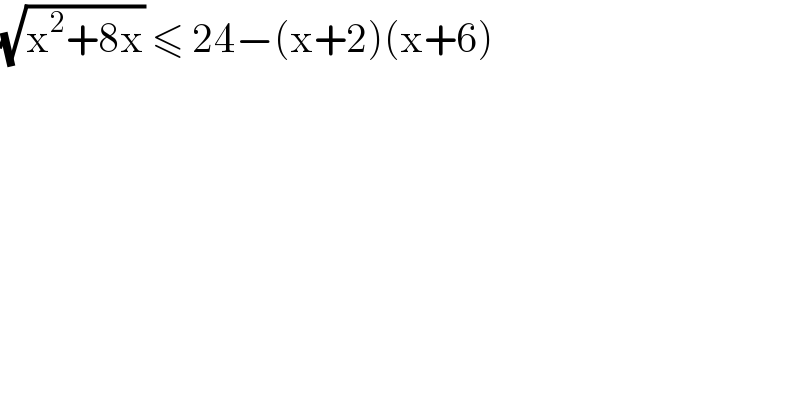
$$\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{8x}}\:\leqslant\:\mathrm{24}−\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{6}\right) \\ $$$$ \\ $$
Answered by TheSupreme last updated on 28/Apr/21
![domain: x<−8 ∨ x>0 { ((24−(x+2)(x+6)>0→12−x^2 −8x>0)),(((12−x^2 −8x)^2 ≥(x^2 +8x))) :} { ((−4−(√(28))<x<−4+(√(28)))),(((12−x^2 −8x)^2 ≥(x^2 +8x))) :} { ((−4−(√(28))<x<−8 ∨ 0<x<−4+(√(28)))),((...)) :} x^2 +8x=u (12−u)^2 ≥u 144−25u+u^2 ≥0 u<((25−(√(625−576)))/2) ∨ x>((25+(√(625−576)))/2) u<((25−7)/2) ∨ u>((25+7)/2) u<9 ∨ x>16 a) x^2 +8x<9 ((−8−(√(64+36)))/2)<x<((−8+(√(64+36)))/2) ((−8−10)/2)<x<((−8+10)/2) −9<x<1 b) x^2 +8x>16 x^2 +8x−16>0 x<((−8−(√(64+64)))/2) ∨ x> ((−8+(√(64+64)))/2) x<−4−4(√2) ∨ x> −4+4(√2) (−∞,−4−4(√2)]∪[−9,1]∪[−4+4(√2),∞) [−4−(√(28)),−8]∪[0,−4+(√(28))] Sol: [−9,−8] ∪[0,1]](https://www.tinkutara.com/question/Q139526.png)
$${domain}:\:{x}<−\mathrm{8}\:\vee\:{x}>\mathrm{0} \\ $$$$\begin{cases}{\mathrm{24}−\left({x}+\mathrm{2}\right)\left({x}+\mathrm{6}\right)>\mathrm{0}\rightarrow\mathrm{12}−{x}^{\mathrm{2}} −\mathrm{8}{x}>\mathrm{0}}\\{\left(\mathrm{12}−{x}^{\mathrm{2}} −\mathrm{8}{x}\right)^{\mathrm{2}} \geqslant\left({x}^{\mathrm{2}} +\mathrm{8}{x}\right)}\end{cases} \\ $$$$\begin{cases}{−\mathrm{4}−\sqrt{\mathrm{28}}<{x}<−\mathrm{4}+\sqrt{\mathrm{28}}}\\{\left(\mathrm{12}−{x}^{\mathrm{2}} −\mathrm{8}{x}\right)^{\mathrm{2}} \geqslant\left({x}^{\mathrm{2}} +\mathrm{8}{x}\right)}\end{cases} \\ $$$$\begin{cases}{−\mathrm{4}−\sqrt{\mathrm{28}}<{x}<−\mathrm{8}\:\vee\:\mathrm{0}<{x}<−\mathrm{4}+\sqrt{\mathrm{28}}}\\{…}\end{cases} \\ $$$${x}^{\mathrm{2}} +\mathrm{8}{x}={u} \\ $$$$\left(\mathrm{12}−{u}\right)^{\mathrm{2}} \geqslant{u} \\ $$$$\mathrm{144}−\mathrm{25}{u}+{u}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$${u}<\frac{\mathrm{25}−\sqrt{\mathrm{625}−\mathrm{576}}}{\mathrm{2}}\:\vee\:{x}>\frac{\mathrm{25}+\sqrt{\mathrm{625}−\mathrm{576}}}{\mathrm{2}} \\ $$$${u}<\frac{\mathrm{25}−\mathrm{7}}{\mathrm{2}}\:\vee\:{u}>\frac{\mathrm{25}+\mathrm{7}}{\mathrm{2}} \\ $$$${u}<\mathrm{9}\:\vee\:{x}>\mathrm{16} \\ $$$$\left.{a}\right)\:{x}^{\mathrm{2}} +\mathrm{8}{x}<\mathrm{9} \\ $$$$\:\:\:\frac{−\mathrm{8}−\sqrt{\mathrm{64}+\mathrm{36}}}{\mathrm{2}}<{x}<\frac{−\mathrm{8}+\sqrt{\mathrm{64}+\mathrm{36}}}{\mathrm{2}} \\ $$$$\:\:\:\frac{−\mathrm{8}−\mathrm{10}}{\mathrm{2}}<{x}<\frac{−\mathrm{8}+\mathrm{10}}{\mathrm{2}} \\ $$$$\:\:\:−\mathrm{9}<{x}<\mathrm{1} \\ $$$$\left.{b}\right)\:{x}^{\mathrm{2}} +\mathrm{8}{x}>\mathrm{16} \\ $$$$\:\:\:{x}^{\mathrm{2}} +\mathrm{8}{x}−\mathrm{16}>\mathrm{0} \\ $$$$\:\:\:{x}<\frac{−\mathrm{8}−\sqrt{\mathrm{64}+\mathrm{64}}}{\mathrm{2}}\:\vee\:{x}>\:\frac{−\mathrm{8}+\sqrt{\mathrm{64}+\mathrm{64}}}{\mathrm{2}} \\ $$$$\:\:\:{x}<−\mathrm{4}−\mathrm{4}\sqrt{\mathrm{2}}\:\:\:\vee\:{x}>\:−\mathrm{4}+\mathrm{4}\sqrt{\mathrm{2}} \\ $$$$\left(−\infty,−\mathrm{4}−\mathrm{4}\sqrt{\mathrm{2}}\right]\cup\left[−\mathrm{9},\mathrm{1}\right]\cup\left[−\mathrm{4}+\mathrm{4}\sqrt{\mathrm{2}},\infty\right) \\ $$$$\left[−\mathrm{4}−\sqrt{\mathrm{28}},−\mathrm{8}\right]\cup\left[\mathrm{0},−\mathrm{4}+\sqrt{\mathrm{28}}\right] \\ $$$${Sol}:\:\left[−\mathrm{9},−\mathrm{8}\right]\:\cup\left[\mathrm{0},\mathrm{1}\right]\: \\ $$
