Question Number 73964 by arkanmath7@gmail.com last updated on 17/Nov/19
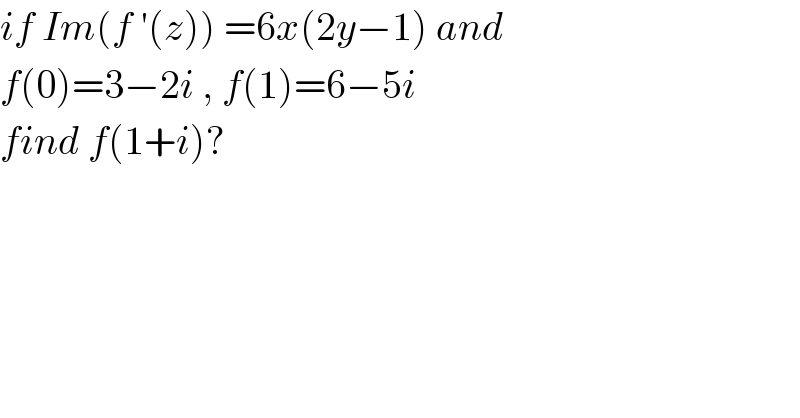
$${if}\:{Im}\left({f}\:'\left({z}\right)\right)\:=\mathrm{6}{x}\left(\mathrm{2}{y}−\mathrm{1}\right)\:{and}\: \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{3}−\mathrm{2}{i}\:,\:{f}\left(\mathrm{1}\right)=\mathrm{6}−\mathrm{5}{i}\: \\ $$$${find}\:{f}\left(\mathrm{1}+{i}\right)? \\ $$
Answered by mind is power last updated on 17/Nov/19

$$\mathrm{f}'\left(\mathrm{z}\right)\:\mathrm{is}\:\frac{\mathrm{df}}{\mathrm{dz}}..? \\ $$$$ \\ $$
Commented by arkanmath7@gmail.com last updated on 17/Nov/19

$${yes} \\ $$
Answered by mind is power last updated on 17/Nov/19

$$\mathrm{f}\left(\mathrm{x}+\mathrm{iy}\right)=\mathrm{p}\left(\mathrm{x},\mathrm{y}\right)+\mathrm{iQ}\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\mathrm{f}'\left(\mathrm{z}\right)=\frac{\partial}{\partial\mathrm{z}}\left(\mathrm{f}\left(\mathrm{z}\right)\right) \\ $$$$\frac{\partial}{\partial\mathrm{z}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\partial}{\partial\mathrm{x}}−\mathrm{i}\frac{\partial}{\partial\mathrm{y}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\partial\mathrm{p}}{\partial\mathrm{x}}+\frac{\partial\mathrm{Q}}{\partial\mathrm{p}}\right)−\frac{\mathrm{i}}{\mathrm{2}}\left(\frac{\partial\mathrm{p}}{\partial\mathrm{y}}−\frac{\partial\mathrm{Q}}{\partial\mathrm{x}}\right) \\ $$$$\mathrm{Im}\left(\mathrm{f}'\left(\mathrm{z}\right)\right)=\mathrm{imf}'\left(\mathrm{x}+\mathrm{iy}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\partial\mathrm{Q}}{\partial\mathrm{x}}−\frac{\partial\mathrm{p}}{\partial\mathrm{y}}\right)=\mathrm{6x}\left(\mathrm{2y}−\mathrm{1}\right)…..\mathrm{E} \\ $$$$\mathrm{f}\:\mathrm{holomorphic}\Rightarrow\frac{\partial\mathrm{p}}{\partial\mathrm{x}}+\mathrm{i}\frac{\partial\mathrm{Q}}{\partial\mathrm{x}}=−\mathrm{i}\frac{\partial\mathrm{p}}{\partial\mathrm{y}}+\frac{\partial\mathrm{Q}}{\partial\mathrm{y}} \\ $$$$\Rightarrow\frac{\partial\mathrm{Q}}{\partial\mathrm{x}}=−\frac{\partial\mathrm{P}}{\partial\mathrm{y}}\Rightarrow\mathrm{E}\frac{\partial\mathrm{Q}}{\partial\mathrm{x}}=\mathrm{12xy}−\mathrm{6x}\Rightarrow\mathrm{Q}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{6x}^{\mathrm{2}} \mathrm{y}−\mathrm{3x}^{\mathrm{2}} +\mathrm{H}\left(\mathrm{y}\right) \\ $$$$\Rightarrow\mathrm{P}\left(\mathrm{x},\mathrm{y}\right)=−\mathrm{6xy}^{\mathrm{2}} +\mathrm{6xy}+\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\frac{\partial\mathrm{p}}{\partial\mathrm{x}}=\frac{\partial\mathrm{Q}}{\partial\mathrm{y}}\Leftrightarrow−\mathrm{6y}^{\mathrm{2}} +\mathrm{6y}+\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{6x}^{\mathrm{2}} +\mathrm{H}'\left(\mathrm{y}\right) \\ $$$$\Rightarrow\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{6x}^{\mathrm{2}} \Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}^{\mathrm{3}} +\mathrm{c} \\ $$$$\mathrm{H}'\left(\mathrm{y}\right)=−\mathrm{6y}^{\mathrm{2}} +\mathrm{6y}\Rightarrow\mathrm{H}\left(\mathrm{y}\right)=−\mathrm{2y}^{\mathrm{3}} +\mathrm{3y}^{\mathrm{2}} +\mathrm{d} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}+\mathrm{iy}\right)=\left(−\mathrm{6xy}^{\mathrm{2}} +\mathrm{6xy}+\mathrm{2x}^{\mathrm{3}} +\mathrm{c}\right)+\mathrm{i}\left(\mathrm{6x}^{\mathrm{2}} \mathrm{y}−\mathrm{3x}^{\mathrm{2}} −\mathrm{2y}^{\mathrm{3}} +\mathrm{3y}^{\mathrm{2}} +\mathrm{d}\right) \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{6}−\mathrm{5i}, \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{3}−\mathrm{2i}\Rightarrow\mathrm{c}=\mathrm{3},\mathrm{d}=−\mathrm{2} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\left(\mathrm{2}+\mathrm{3}\right)+\mathrm{i}\left(−\mathrm{3}−\mathrm{2}\right)=\mathrm{5}−\mathrm{5i} \\ $$$$\mathrm{f}\:\mathrm{did}'\mathrm{nt}\:\mathrm{exist}\:\mathrm{withe}\:\mathrm{this}\:\mathrm{conditions} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by arkanmath7@gmail.com last updated on 18/Nov/19

$${thmx}\:{sir} \\ $$
Commented by mind is power last updated on 18/Nov/19

$${y}'{re}\:{welcom} \\ $$
