Question Number 139505 by bemath last updated on 28/Apr/21
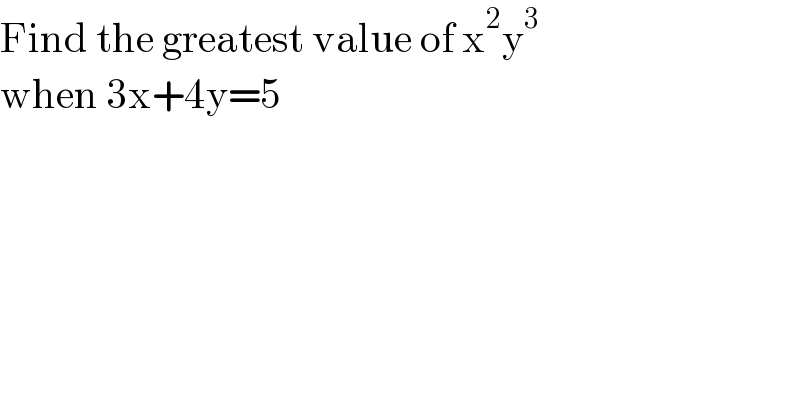
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{3}} \: \\ $$$$\mathrm{when}\:\mathrm{3x}+\mathrm{4y}=\mathrm{5} \\ $$
Commented by mr W last updated on 28/Apr/21
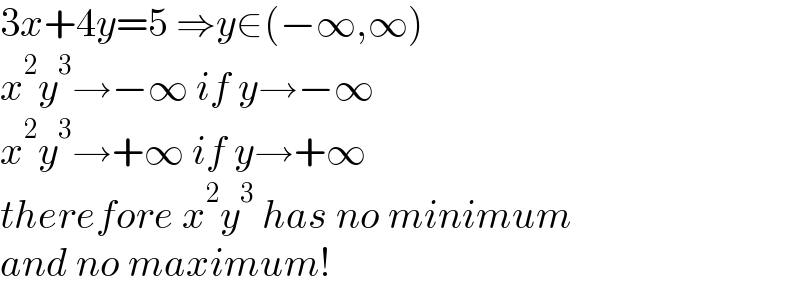
$$\mathrm{3}{x}+\mathrm{4}{y}=\mathrm{5}\:\Rightarrow{y}\in\left(−\infty,\infty\right) \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{3}} \rightarrow−\infty\:{if}\:{y}\rightarrow−\infty \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{3}} \rightarrow+\infty\:{if}\:{y}\rightarrow+\infty \\ $$$${therefore}\:{x}^{\mathrm{2}} {y}^{\mathrm{3}} \:{has}\:{no}\:{minimum}\: \\ $$$${and}\:{no}\:{maximum}! \\ $$
Answered by MJS_new last updated on 28/Apr/21
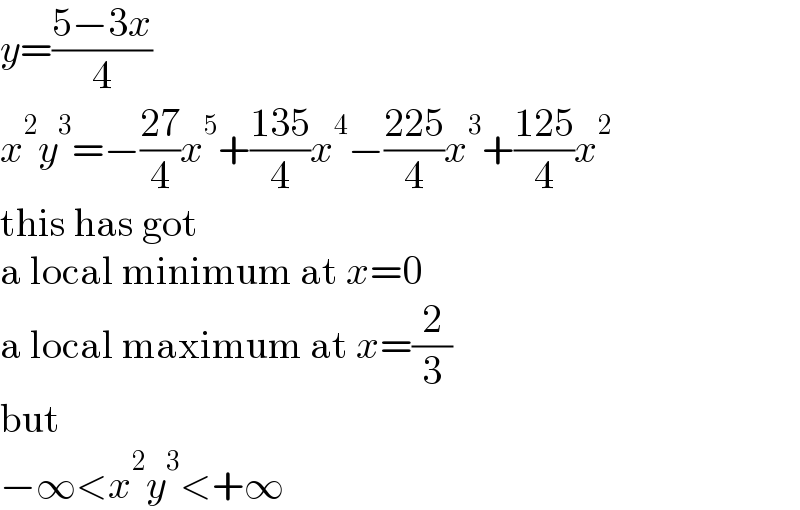
$${y}=\frac{\mathrm{5}−\mathrm{3}{x}}{\mathrm{4}} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{3}} =−\frac{\mathrm{27}}{\mathrm{4}}{x}^{\mathrm{5}} +\frac{\mathrm{135}}{\mathrm{4}}{x}^{\mathrm{4}} −\frac{\mathrm{225}}{\mathrm{4}}{x}^{\mathrm{3}} +\frac{\mathrm{125}}{\mathrm{4}}{x}^{\mathrm{2}} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{got} \\ $$$$\mathrm{a}\:\mathrm{local}\:\mathrm{minimum}\:\mathrm{at}\:{x}=\mathrm{0} \\ $$$$\mathrm{a}\:\mathrm{local}\:\mathrm{maximum}\:\mathrm{at}\:{x}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{but} \\ $$$$−\infty<{x}^{\mathrm{2}} {y}^{\mathrm{3}} <+\infty \\ $$
