Question Number 672 by 123456 last updated on 21/Feb/15
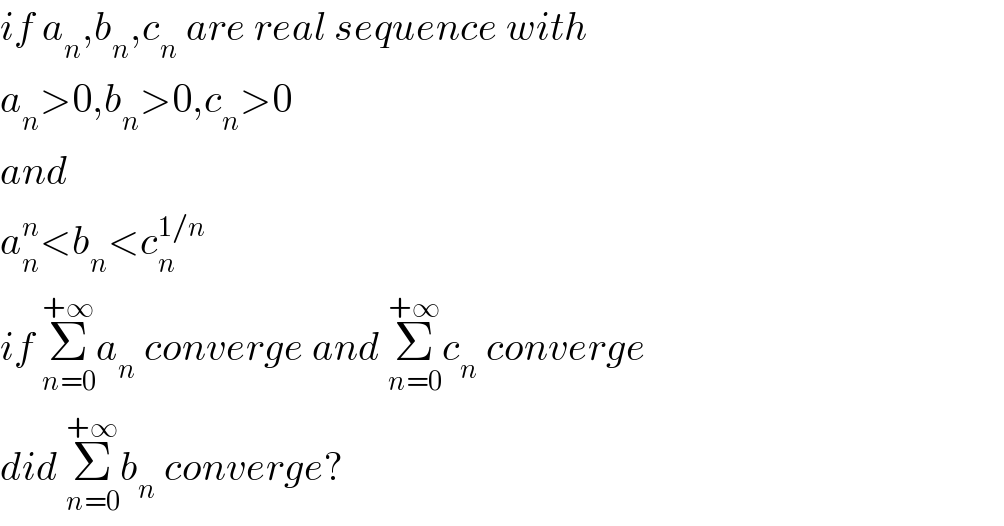
$${if}\:{a}_{{n}} ,{b}_{{n}} ,{c}_{{n}} \:{are}\:{real}\:{sequence}\:{with} \\ $$$${a}_{{n}} >\mathrm{0},{b}_{{n}} >\mathrm{0},{c}_{{n}} >\mathrm{0} \\ $$$${and} \\ $$$${a}_{{n}} ^{{n}} <{b}_{{n}} <{c}_{{n}} ^{\mathrm{1}/{n}} \\ $$$${if}\:\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}{a}_{{n}} \:{converge}\:{and}\:\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}{c}_{{n}} \:{converge} \\ $$$${did}\:\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}{b}_{{n}} \:{converge}? \\ $$
Commented by prakash jain last updated on 22/Feb/15
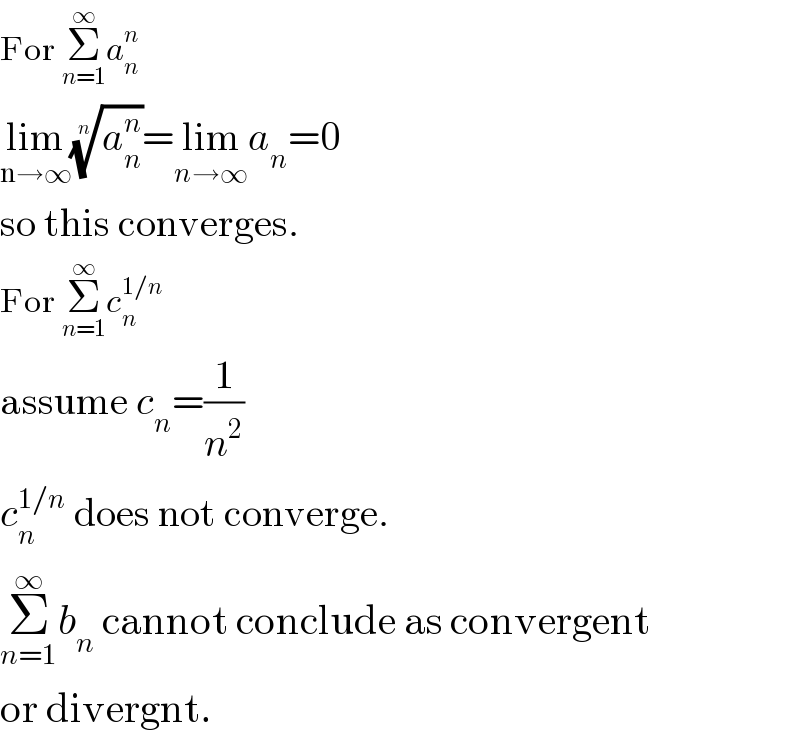
$$\mathrm{For}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{a}_{{n}} ^{{n}} \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\sqrt[{{n}}]{{a}_{{n}} ^{{n}} }=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{a}_{{n}} =\mathrm{0}\: \\ $$$$\mathrm{so}\:\mathrm{this}\:\mathrm{converges}. \\ $$$$\mathrm{For}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{c}_{{n}} ^{\mathrm{1}/{n}} \\ $$$$\mathrm{assume}\:{c}_{{n}} =\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$${c}_{{n}} ^{\mathrm{1}/{n}} \:\mathrm{does}\:\mathrm{not}\:\mathrm{converge}. \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{b}_{{n}} \:\mathrm{cannot}\:\mathrm{conclude}\:\mathrm{as}\:\mathrm{convergent} \\ $$$$\mathrm{or}\:\mathrm{divergnt}. \\ $$
