Question Number 8503 by MNG last updated on 13/Oct/16
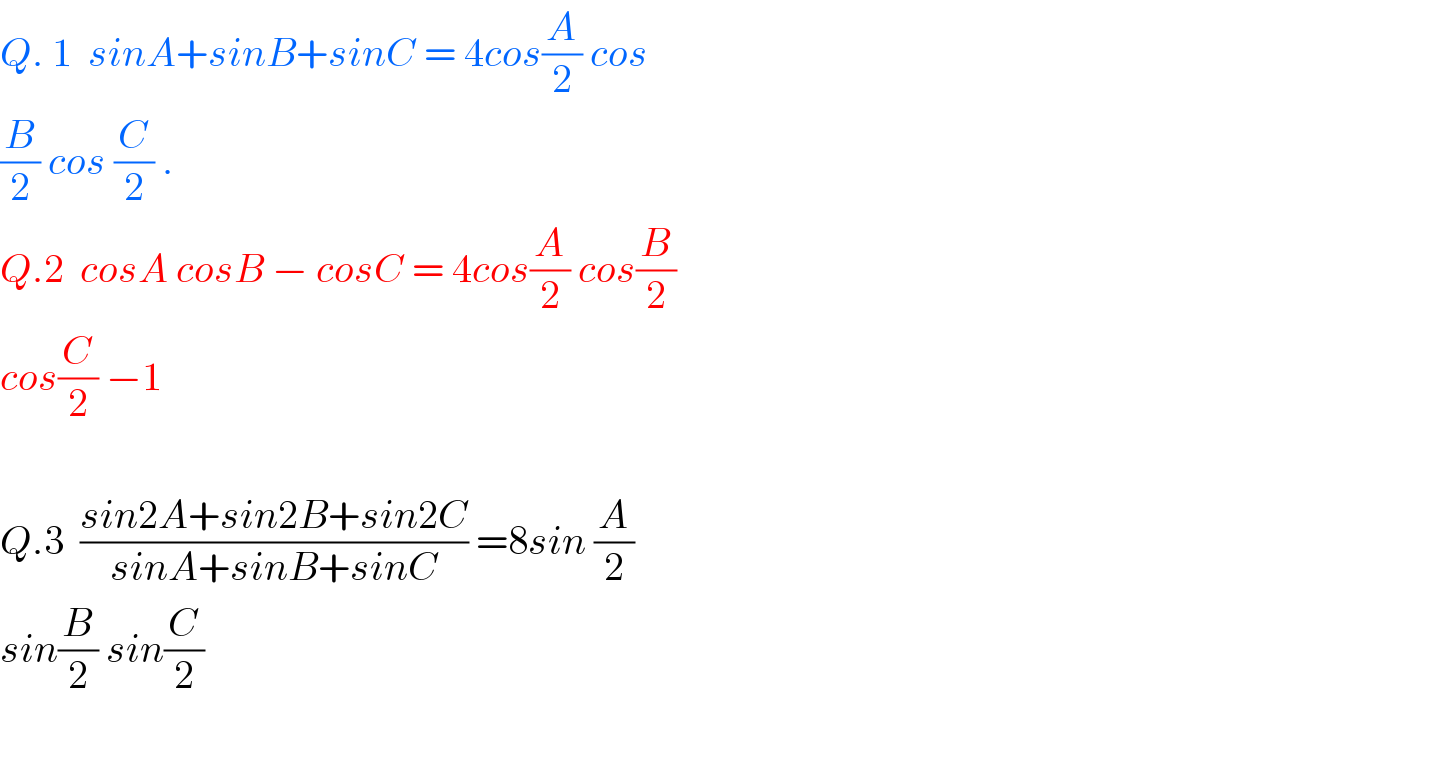
$${Q}.\:\mathrm{1}\:\:{sinA}+{sinB}+{sinC}\:=\:\mathrm{4}{cos}\frac{{A}}{\mathrm{2}}\:{cos} \\ $$$$\frac{{B}}{\mathrm{2}}\:{cos}\:\frac{{C}}{\mathrm{2}}\:. \\ $$$${Q}.\mathrm{2}\:\:{cosA}\:{cosB}\:−\:{cosC}\:=\:\mathrm{4}{cos}\frac{{A}}{\mathrm{2}}\:{cos}\frac{{B}}{\mathrm{2}} \\ $$$${cos}\frac{{C}}{\mathrm{2}}\:−\mathrm{1} \\ $$$$ \\ $$$${Q}.\mathrm{3}\:\:\frac{{sin}\mathrm{2}{A}+{sin}\mathrm{2}{B}+{sin}\mathrm{2}{C}}{{sinA}+{sinB}+{sinC}}\:=\mathrm{8}{sin}\:\frac{{A}}{\mathrm{2}} \\ $$$${sin}\frac{{B}}{\mathrm{2}}\:{sin}\frac{{C}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by sandy_suhendra last updated on 13/Oct/16

$$\mathrm{Is}\:\mathrm{A}+\mathrm{B}+\mathrm{C}=\mathrm{180}°\:? \\ $$
Commented by MNG last updated on 14/Oct/16

$${yes} \\ $$
Answered by prakash jain last updated on 14/Oct/16

$$\mathrm{Q1} \\ $$$$\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:{C} \\ $$$$=\mathrm{2sin}\:\frac{{A}+{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}+\mathrm{sin}\:{C} \\ $$$${A}+{B}+{C}=\pi\Rightarrow\frac{{A}+{B}}{\mathrm{2}}=\frac{\pi}{\mathrm{2}}−\frac{{C}}{\mathrm{2}} \\ $$$$=\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{{C}}{\mathrm{2}}\right)\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}+\mathrm{2sin}\:\frac{{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{C}}{\mathrm{2}} \\ $$$$=\mathrm{2cos}\:\frac{{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}+\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{{A}+{B}}{\mathrm{2}}\right)\mathrm{cos}\:\frac{{C}}{\mathrm{2}} \\ $$$$=\mathrm{2cos}\:\frac{{C}}{\mathrm{2}}\left\{\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}+\mathrm{cos}\:\frac{{A}+{B}}{\mathrm{2}}\right\} \\ $$$$=\mathrm{2cos}\:\frac{{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{2}} \\ $$$${formula} \\ $$$$\mathrm{sin}\:{A}+\mathrm{sin}\:{B}=\mathrm{2sin}\:\frac{{A}+{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:{A}+\mathrm{cos}\:{B}=\mathrm{2cos}\:\frac{{A}+{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}} \\ $$
