Menu Close

show-that-0-cos-x-e-2pi-x-1-dx-1-e-e-1-2-

Tinku Tara 0 Comments
Pin




Question Number 139612 by 676597498 last updated on 29/Apr/21
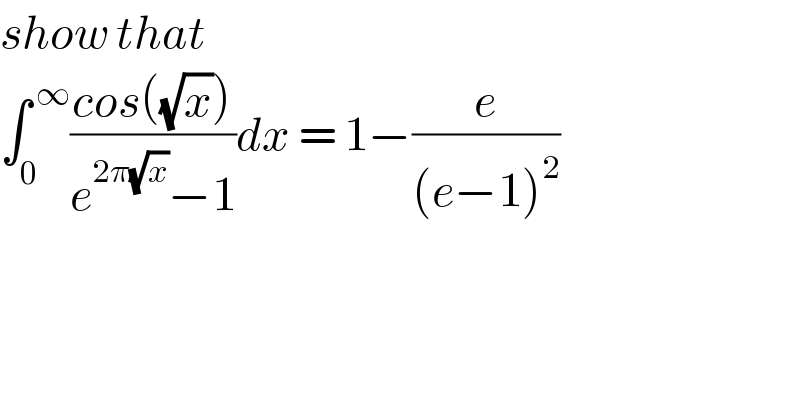
show that ∫_0 ^( ∞) ((cos((√x)))/(e^(2π(√x)) −1))dx = 1−(e/((e−1)^2 ))
$${show}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\left(\sqrt{{x}}\right)}{{e}^{\mathrm{2}\pi\sqrt{{x}}} −\mathrm{1}}{dx}\:=\:\mathrm{1}−\frac{{e}}{\left({e}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Answered by Dwaipayan Shikari last updated on 29/Apr/21
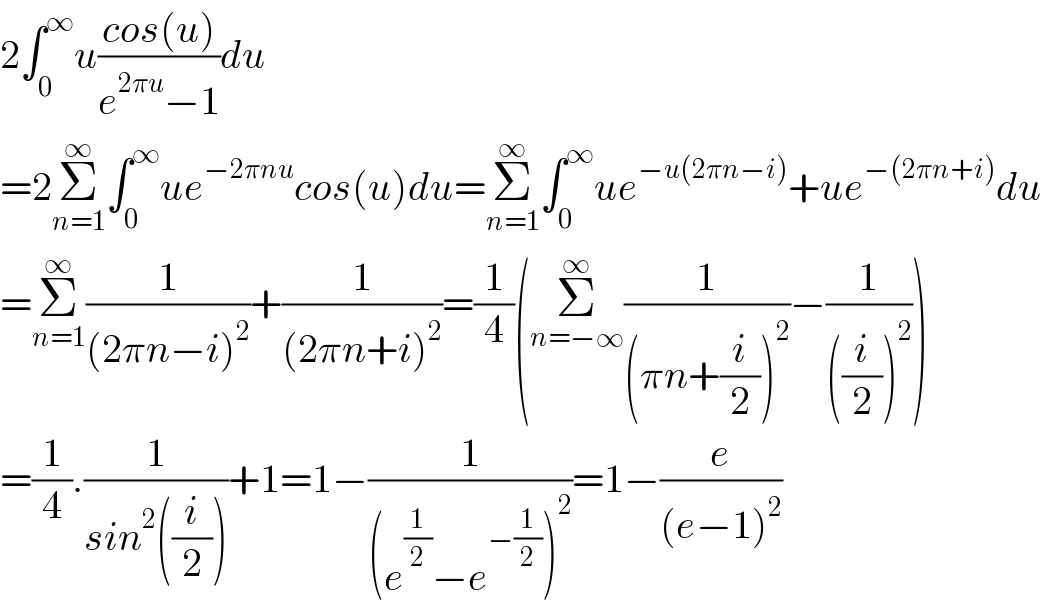
2∫_0 ^∞ u((cos(u))/(e^(2πu) −1))du =2Σ_(n=1) ^∞ ∫_0 ^∞ ue^(−2πnu) cos(u)du=Σ_(n=1) ^∞ ∫_0 ^∞ ue^(−u(2πn−i)) +ue^(−(2πn+i)) du =Σ_(n=1) ^∞ (1/((2πn−i)^2 ))+(1/((2πn+i)^2 ))=(1/4)(Σ_(n=−∞) ^∞ (1/((πn+(i/2))^2 ))−(1/(((i/2))^2 ))) =(1/4).(1/(sin^2 ((i/2))))+1=1−(1/((e^(1/2) −e^(−(1/2)) )^2 ))=1−(e/((e−1)^2 ))
$$\mathrm{2}\int_{\mathrm{0}} ^{\infty} {u}\frac{{cos}\left({u}\right)}{{e}^{\mathrm{2}\pi{u}} −\mathrm{1}}{du} \\ $$$$=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {ue}^{−\mathrm{2}\pi{nu}} {cos}\left({u}\right){du}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {ue}^{−{u}\left(\mathrm{2}\pi{n}−{i}\right)} +{ue}^{−\left(\mathrm{2}\pi{n}+{i}\right)} {du} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}\pi{n}−{i}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{2}\pi{n}+{i}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}\left(\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\pi{n}+\frac{{i}}{\mathrm{2}}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\frac{{i}}{\mathrm{2}}\right)^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \left(\frac{{i}}{\mathrm{2}}\right)}+\mathrm{1}=\mathrm{1}−\frac{\mathrm{1}}{\left({e}^{\frac{\mathrm{1}}{\mathrm{2}}} −{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\mathrm{2}} }=\mathrm{1}−\frac{{e}}{\left({e}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by 676597498 last updated on 29/Apr/21
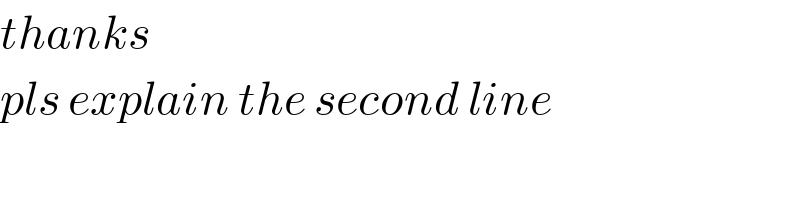
thanks pls explain the second line
$${thanks} \\ $$$${pls}\:{explain}\:{the}\:{second}\:{line} \\ $$
Commented by Dwaipayan Shikari last updated on 30/Apr/21
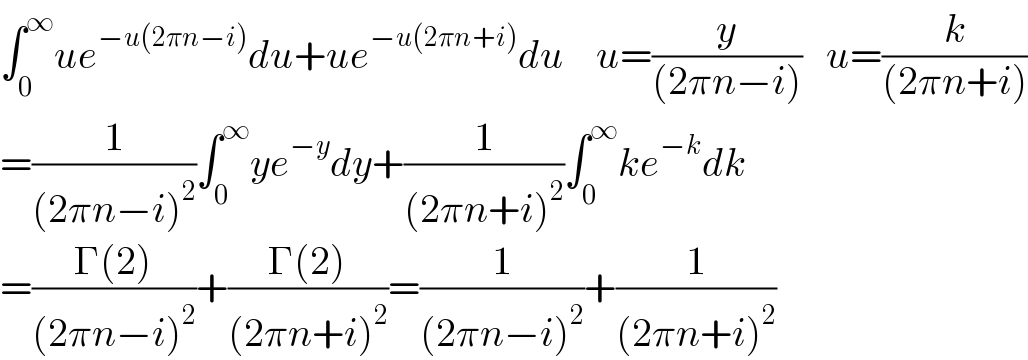
∫_0 ^∞ ue^(−u(2πn−i)) du+ue^(−u(2πn+i)) du u=(y/((2πn−i))) u=(k/((2πn+i))) =(1/((2πn−i)^2 ))∫_0 ^∞ ye^(−y) dy+(1/((2πn+i)^2 ))∫_0 ^∞ ke^(−k) dk =((Γ(2))/((2πn−i)^2 ))+((Γ(2))/((2πn+i)^2 ))=(1/((2πn−i)^2 ))+(1/((2πn+i)^2 ))
$$\int_{\mathrm{0}} ^{\infty} {ue}^{−{u}\left(\mathrm{2}\pi{n}−{i}\right)} {du}+{ue}^{−{u}\left(\mathrm{2}\pi{n}+{i}\right)} {du}\:\:\:\:{u}=\frac{{y}}{\left(\mathrm{2}\pi{n}−{i}\right)}\:\:\:{u}=\frac{{k}}{\left(\mathrm{2}\pi{n}+{i}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2}\pi{n}−{i}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} {ye}^{−{y}} {dy}+\frac{\mathrm{1}}{\left(\mathrm{2}\pi{n}+{i}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} {ke}^{−{k}} {dk} \\ $$$$=\frac{\Gamma\left(\mathrm{2}\right)}{\left(\mathrm{2}\pi{n}−{i}\right)^{\mathrm{2}} }+\frac{\Gamma\left(\mathrm{2}\right)}{\left(\mathrm{2}\pi{n}+{i}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\left(\mathrm{2}\pi{n}−{i}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{2}\pi{n}+{i}\right)^{\mathrm{2}} } \\ $$
Commented by 676597498 last updated on 30/Apr/21
sorry sir i understood this i meant the third line sir
$${sorry}\:{sir}\:{i}\:{understood}\:{this} \\ $$$${i}\:{meant}\:{the}\:{third}\:{line}\:{sir} \\ $$
Commented by Dwaipayan Shikari last updated on 30/Apr/21
Generally sinx=xΠ_(n=1) ^∞ (1−(x^2 /(π^2 n^2 ))) log(sinx)=log(x)+Σlog(1−(x/(πn)))+Σlog(1+(x/(πn))) Differentiate both sides respect to x ((cosx)/(sinx))=(1/x)+Σ((−(1/(πn)))/(1−(x/(πn))))+Σ((1/(πn))/(1+(x/(πn)))) cotx=(1/x)+Σ_(n=1) ^∞ (1/(x−πn))+Σ_(n=1) ^∞ (1/(x+πn)) cotx=Σ_(n=−∞) ^∞ (1/(x+πn)) ⇒(1/(sin^2 x))=Σ_(n=−∞) ^∞ (1/((x+πn)^2 )) (Differentiate again)
$${Generally} \\ $$$${sinx}={x}\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\pi^{\mathrm{2}} {n}^{\mathrm{2}} }\right) \\ $$$${log}\left({sinx}\right)={log}\left({x}\right)+\Sigma{log}\left(\mathrm{1}−\frac{{x}}{\pi{n}}\right)+\Sigma{log}\left(\mathrm{1}+\frac{{x}}{\pi{n}}\right) \\ $$$${Differentiate}\:{both}\:{sides}\:{respect}\:{to}\:{x} \\ $$$$\frac{{cosx}}{{sinx}}=\frac{\mathrm{1}}{{x}}+\Sigma\frac{−\frac{\mathrm{1}}{\pi{n}}}{\mathrm{1}−\frac{{x}}{\pi{n}}}+\Sigma\frac{\frac{\mathrm{1}}{\pi{n}}}{\mathrm{1}+\frac{{x}}{\pi{n}}} \\ $$$${cotx}=\frac{\mathrm{1}}{{x}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{x}−\pi{n}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{x}+\pi{n}} \\ $$$${cotx}=\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{x}+\pi{n}}\:\Rightarrow\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {x}}=\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({x}+\pi{n}\right)^{\mathrm{2}} }\:\left({Differentiate}\:{again}\right) \\ $$
Commented by mnjuly1970 last updated on 30/Apr/21
thanks alot...
$${thanks}\:{alot}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *