Question Number 8602 by tawakalitu last updated on 17/Oct/16
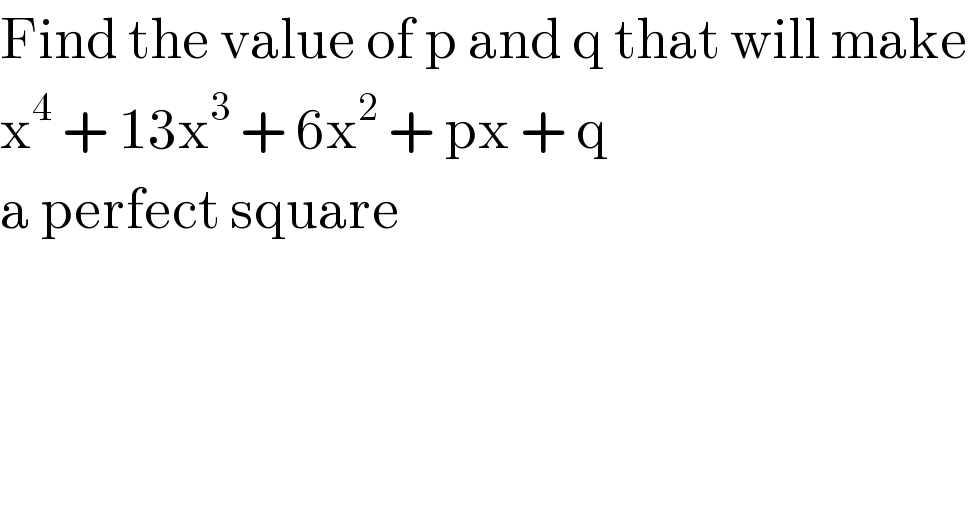
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}\:\mathrm{that}\:\mathrm{will}\:\mathrm{make} \\ $$$$\mathrm{x}^{\mathrm{4}} \:+\:\mathrm{13x}^{\mathrm{3}} \:+\:\mathrm{6x}^{\mathrm{2}} \:+\:\mathrm{px}\:+\:\mathrm{q}\:\: \\ $$$$\mathrm{a}\:\mathrm{perfect}\:\mathrm{square} \\ $$
Answered by sandy_suhendra last updated on 17/Oct/16
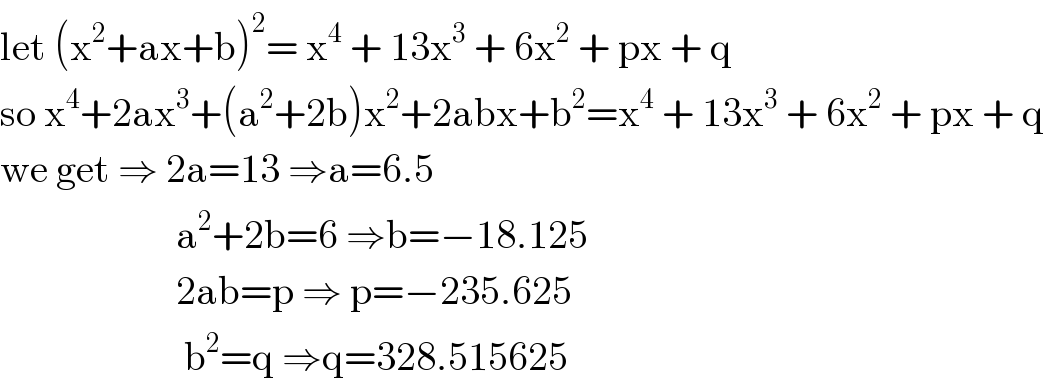
$$\mathrm{let}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{b}\right)^{\mathrm{2}} =\:\mathrm{x}^{\mathrm{4}} \:+\:\mathrm{13x}^{\mathrm{3}} \:+\:\mathrm{6x}^{\mathrm{2}} \:+\:\mathrm{px}\:+\:\mathrm{q}\: \\ $$$$\mathrm{so}\:\mathrm{x}^{\mathrm{4}} +\mathrm{2ax}^{\mathrm{3}} +\left(\mathrm{a}^{\mathrm{2}} +\mathrm{2b}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{2abx}+\mathrm{b}^{\mathrm{2}} =\mathrm{x}^{\mathrm{4}} \:+\:\mathrm{13x}^{\mathrm{3}} \:+\:\mathrm{6x}^{\mathrm{2}} \:+\:\mathrm{px}\:+\:\mathrm{q} \\ $$$$\mathrm{we}\:\mathrm{get}\:\Rightarrow\:\mathrm{2a}=\mathrm{13}\:\Rightarrow\mathrm{a}=\mathrm{6}.\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}^{\mathrm{2}} +\mathrm{2b}=\mathrm{6}\:\Rightarrow\mathrm{b}=−\mathrm{18}.\mathrm{125} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2ab}=\mathrm{p}\:\Rightarrow\:\mathrm{p}=−\mathrm{235}.\mathrm{625} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{b}^{\mathrm{2}} =\mathrm{q}\:\Rightarrow\mathrm{q}=\mathrm{328}.\mathrm{515625} \\ $$
Commented by tawakalitu last updated on 17/Oct/16
$$\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir} \\ $$
