Question Number 66225 by Rio Michael last updated on 11/Aug/19
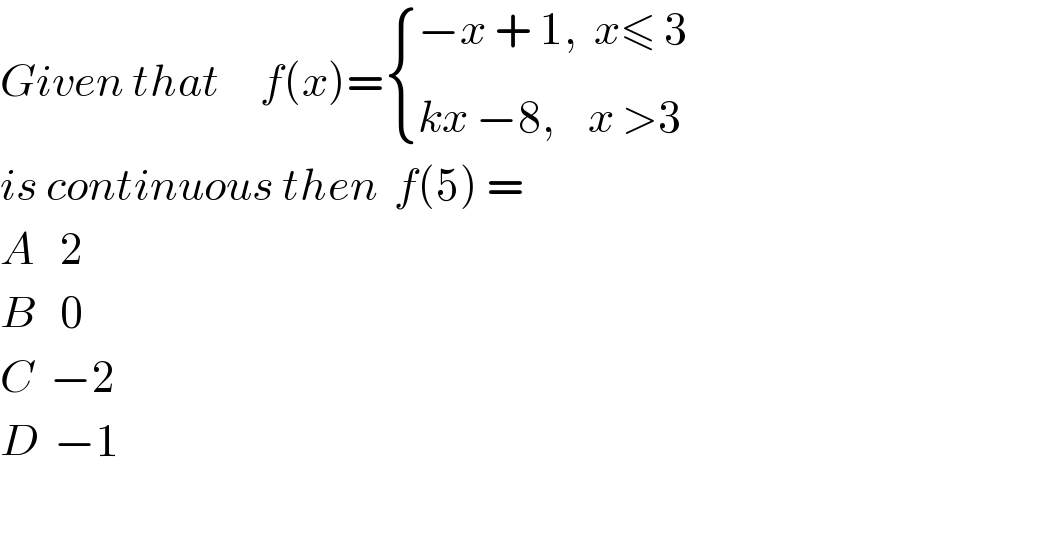
$${Given}\:{that}\:\:\:\:\:{f}\left({x}\right)=\begin{cases}{−{x}\:+\:\mathrm{1},\:\:{x}\leqslant\:\mathrm{3}_{} }\\{{kx}\:−\mathrm{8},\:\:\:\:{x}\:>\mathrm{3}}\end{cases} \\ $$$${is}\:{continuous}\:{then}\:\:{f}\left(\mathrm{5}\right)\:=\: \\ $$$${A}\:\:\:\mathrm{2} \\ $$$${B}\:\:\:\mathrm{0} \\ $$$${C}\:\:−\mathrm{2} \\ $$$${D}\:\:−\mathrm{1} \\ $$$$ \\ $$
Commented by Prithwish sen last updated on 11/Aug/19

$$\mathrm{A}.\:\:\mathrm{2} \\ $$
Commented by mathmax by abdo last updated on 11/Aug/19
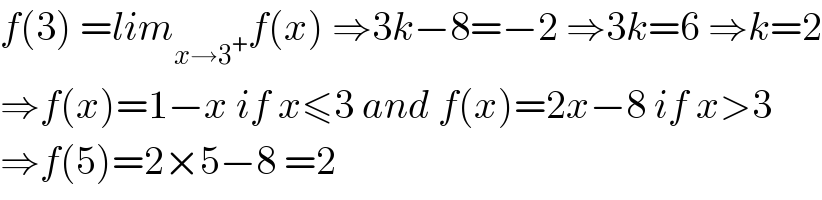
$${f}\left(\mathrm{3}\right)\:={lim}_{{x}\rightarrow\mathrm{3}^{+} } {f}\left({x}\right)\:\Rightarrow\mathrm{3}{k}−\mathrm{8}=−\mathrm{2}\:\Rightarrow\mathrm{3}{k}=\mathrm{6}\:\Rightarrow{k}=\mathrm{2} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{1}−{x}\:{if}\:{x}\leqslant\mathrm{3}\:{and}\:{f}\left({x}\right)=\mathrm{2}{x}−\mathrm{8}\:{if}\:{x}>\mathrm{3} \\ $$$$\Rightarrow{f}\left(\mathrm{5}\right)=\mathrm{2}×\mathrm{5}−\mathrm{8}\:=\mathrm{2} \\ $$
Answered by som(math1967) last updated on 11/Aug/19
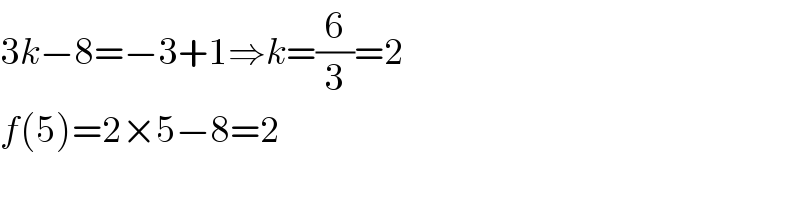
$$\mathrm{3}{k}−\mathrm{8}=−\mathrm{3}+\mathrm{1}\Rightarrow{k}=\frac{\mathrm{6}}{\mathrm{3}}=\mathrm{2} \\ $$$${f}\left(\mathrm{5}\right)=\mathrm{2}×\mathrm{5}−\mathrm{8}=\mathrm{2} \\ $$
