Question-74246

Question Number 74246 by TawaTawa last updated on 20/Nov/19

Answered by MJS last updated on 20/Nov/19

1 2 49 ... 1 25 26 24 triples 2 3 47 ... 2 24 26 22 triples 3 4 45 ... 3 24 25 21 triples starting with 4: 19 starting with 5: 18 6: 16 7: 15 8: 13 9: 12 10: 10 11: 9 12: 7 13: 6 14: 4 15: 3 16: 1 [16 17 19] ⇒ 200 triples

$$\mathrm{1}\:\mathrm{2}\:\mathrm{49} \\ $$$$… \\ $$$$\mathrm{1}\:\mathrm{25}\:\mathrm{26} \\ $$$$\mathrm{24}\:\mathrm{triples} \\ $$$$\mathrm{2}\:\mathrm{3}\:\mathrm{47} \\ $$$$… \\ $$$$\mathrm{2}\:\mathrm{24}\:\mathrm{26} \\ $$$$\mathrm{22}\:\mathrm{triples} \\ $$$$\mathrm{3}\:\mathrm{4}\:\mathrm{45} \\ $$$$… \\ $$$$\mathrm{3}\:\mathrm{24}\:\mathrm{25} \\ $$$$\mathrm{21}\:\mathrm{triples} \\ $$$$ \\ $$$$\mathrm{starting}\:\mathrm{with}\:\mathrm{4}:\:\mathrm{19} \\ $$$$\mathrm{starting}\:\mathrm{with}\:\mathrm{5}:\:\mathrm{18} \\ $$$$\mathrm{6}:\:\mathrm{16} \\ $$$$\mathrm{7}:\:\mathrm{15} \\ $$$$\mathrm{8}:\:\mathrm{13} \\ $$$$\mathrm{9}:\:\mathrm{12} \\ $$$$\mathrm{10}:\:\mathrm{10} \\ $$$$\mathrm{11}:\:\mathrm{9} \\ $$$$\mathrm{12}:\:\mathrm{7} \\ $$$$\mathrm{13}:\:\mathrm{6} \\ $$$$\mathrm{14}:\:\mathrm{4} \\ $$$$\mathrm{15}:\:\mathrm{3} \\ $$$$\mathrm{16}:\:\mathrm{1}\:\left[\mathrm{16}\:\mathrm{17}\:\mathrm{19}\right] \\ $$$$ \\ $$$$\Rightarrow \\ $$$$\mathrm{200}\:\mathrm{triples} \\ $$

Commented by mind is power last updated on 21/Nov/19

$${Nice} \\ $$

Commented by TawaTawa last updated on 21/Nov/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{your}\:\mathrm{sir} \\ $$

Answered by mind is power last updated on 21/Nov/19

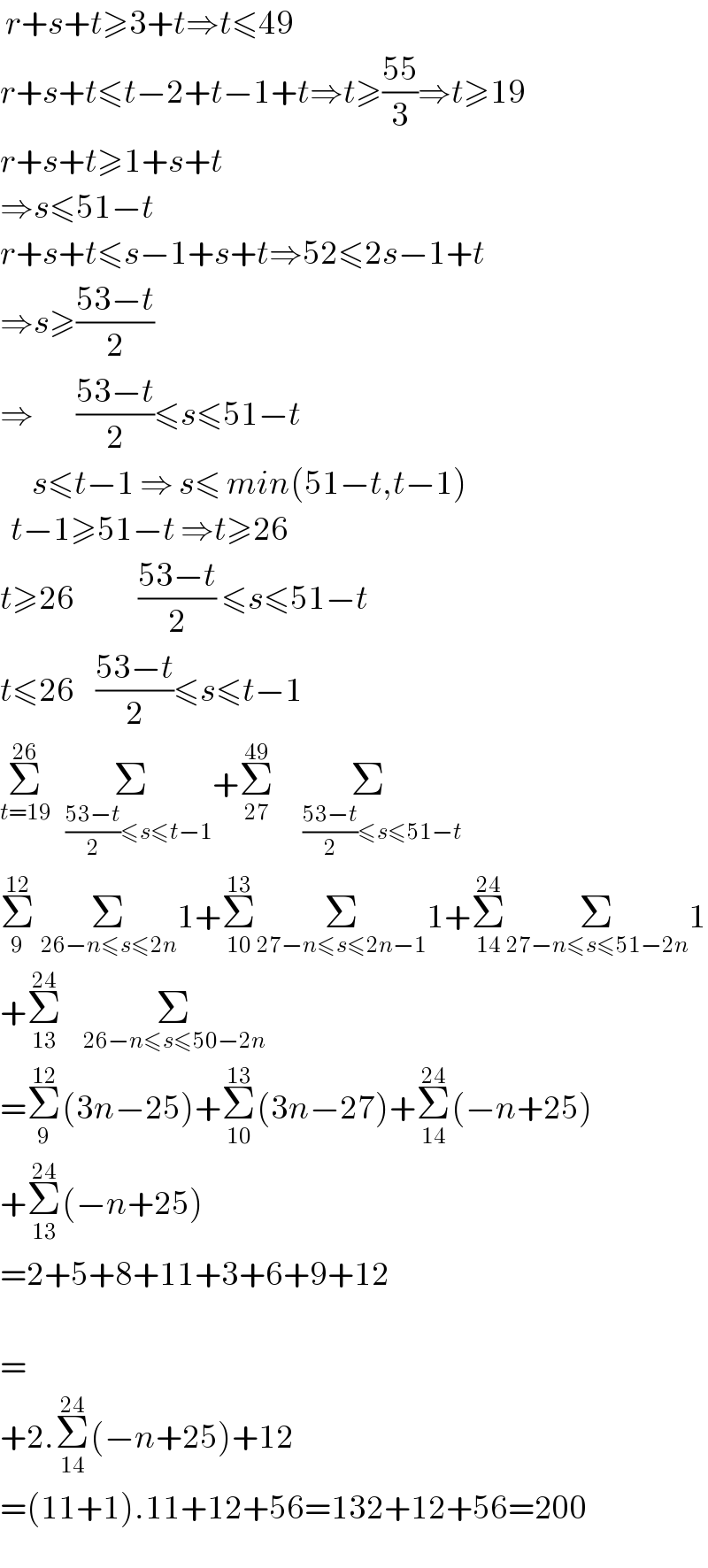
r+s+t≥3+t⇒t≤49 r+s+t≤t−2+t−1+t⇒t≥((55)/3)⇒t≥19 r+s+t≥1+s+t ⇒s≤51−t r+s+t≤s−1+s+t⇒52≤2s−1+t ⇒s≥((53−t)/2) ⇒ ((53−t)/2)≤s≤51−t s≤t−1 ⇒ s≤ min(51−t,t−1) t−1≥51−t ⇒t≥26 t≥26 ((53−t)/2) ≤s≤51−t t≤26 ((53−t)/2)≤s≤t−1 Σ_(t=19) ^(26) Σ_( ((53−t)/2)≤s≤t−1) +Σ_(27) ^(49) Σ_( ((53−t)/2)≤s≤51−t) Σ_9 ^(12) Σ_(26−n≤s≤2n) 1+Σ_(10) ^(13) Σ_(27−n≤s≤2n−1) 1+Σ_(14) ^(24) Σ_(27−n≤s≤51−2n) 1 +Σ_(13) ^(24) Σ_(26−n≤s≤50−2n) =Σ_9 ^(12) (3n−25)+Σ_(10) ^(13) (3n−27)+Σ_(14) ^(24) (−n+25) +Σ_(13) ^(24) (−n+25) =2+5+8+11+3+6+9+12 = +2.Σ_(14) ^(24) (−n+25)+12 =(11+1).11+12+56=132+12+56=200

$$\:{r}+{s}+{t}\geqslant\mathrm{3}+{t}\Rightarrow{t}\leqslant\mathrm{49} \\ $$$${r}+{s}+{t}\leqslant{t}−\mathrm{2}+{t}−\mathrm{1}+{t}\Rightarrow{t}\geqslant\frac{\mathrm{55}}{\mathrm{3}}\Rightarrow{t}\geqslant\mathrm{19} \\ $$$${r}+{s}+{t}\geqslant\mathrm{1}+{s}+{t} \\ $$$$\Rightarrow{s}\leqslant\mathrm{51}−{t} \\ $$$${r}+{s}+{t}\leqslant{s}−\mathrm{1}+{s}+{t}\Rightarrow\mathrm{52}\leqslant\mathrm{2}{s}−\mathrm{1}+{t} \\ $$$$\Rightarrow{s}\geqslant\frac{\mathrm{53}−{t}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\frac{\mathrm{53}−{t}}{\mathrm{2}}\leqslant{s}\leqslant\mathrm{51}−{t} \\ $$$$\:\:\:\:\:\:{s}\leqslant{t}−\mathrm{1}\:\Rightarrow\:{s}\leqslant\:{min}\left(\mathrm{51}−{t},{t}−\mathrm{1}\right) \\ $$$$\:\:{t}−\mathrm{1}\geqslant\mathrm{51}−{t}\:\Rightarrow{t}\geqslant\mathrm{26} \\ $$$${t}\geqslant\mathrm{26}\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{53}−{t}}{\mathrm{2}}\:\leqslant{s}\leqslant\mathrm{51}−{t} \\ $$$${t}\leqslant\mathrm{26}\:\:\:\:\frac{\mathrm{53}−{t}}{\mathrm{2}}\leqslant{s}\leqslant{t}−\mathrm{1} \\ $$$$\underset{{t}=\mathrm{19}} {\overset{\mathrm{26}} {\sum}}\underset{\:\:\:\:\frac{\mathrm{53}−{t}}{\mathrm{2}}\leqslant{s}\leqslant{t}−\mathrm{1}} {\sum}+\underset{\mathrm{27}} {\overset{\mathrm{49}} {\sum}}\underset{\:\:\:\:\:\:\:\:\frac{\mathrm{53}−{t}}{\mathrm{2}}\leqslant{s}\leqslant\mathrm{51}−{t}} {\sum} \\ $$$$\underset{\mathrm{9}} {\overset{\mathrm{12}} {\sum}}\:\underset{\mathrm{26}−{n}\leqslant{s}\leqslant\mathrm{2}{n}} {\sum}\mathrm{1}+\underset{\mathrm{10}} {\overset{\mathrm{13}} {\sum}}\underset{\mathrm{27}−{n}\leqslant{s}\leqslant\mathrm{2}{n}−\mathrm{1}} {\sum}\mathrm{1}+\underset{\mathrm{14}} {\overset{\mathrm{24}} {\sum}}\underset{\mathrm{27}−{n}\leqslant{s}\leqslant\mathrm{51}−\mathrm{2}{n}} {\sum}\mathrm{1} \\ $$$$+\underset{\mathrm{13}} {\overset{\mathrm{24}} {\sum}}\:\:\:\:\underset{\mathrm{26}−{n}\leqslant{s}\leqslant\mathrm{50}−\mathrm{2}{n}} {\sum} \\ $$$$=\underset{\mathrm{9}} {\overset{\mathrm{12}} {\sum}}\left(\mathrm{3}{n}−\mathrm{25}\right)+\underset{\mathrm{10}} {\overset{\mathrm{13}} {\sum}}\left(\mathrm{3}{n}−\mathrm{27}\right)+\underset{\mathrm{14}} {\overset{\mathrm{24}} {\sum}}\left(−{n}+\mathrm{25}\right) \\ $$$$+\underset{\mathrm{13}} {\overset{\mathrm{24}} {\sum}}\left(−{n}+\mathrm{25}\right) \\ $$$$=\mathrm{2}+\mathrm{5}+\mathrm{8}+\mathrm{11}+\mathrm{3}+\mathrm{6}+\mathrm{9}+\mathrm{12} \\ $$$$ \\ $$$$= \\ $$$$+\mathrm{2}.\underset{\mathrm{14}} {\overset{\mathrm{24}} {\sum}}\left(−{n}+\mathrm{25}\right)+\mathrm{12} \\ $$$$=\left(\mathrm{11}+\mathrm{1}\right).\mathrm{11}+\mathrm{12}+\mathrm{56}=\mathrm{132}+\mathrm{12}+\mathrm{56}=\mathrm{200} \\ $$

Commented by TawaTawa last updated on 21/Nov/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mind is power last updated on 21/Nov/19

$${y}'{re}\:{welcom} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply