Question Number 66253 by mathmax by abdo last updated on 11/Aug/19
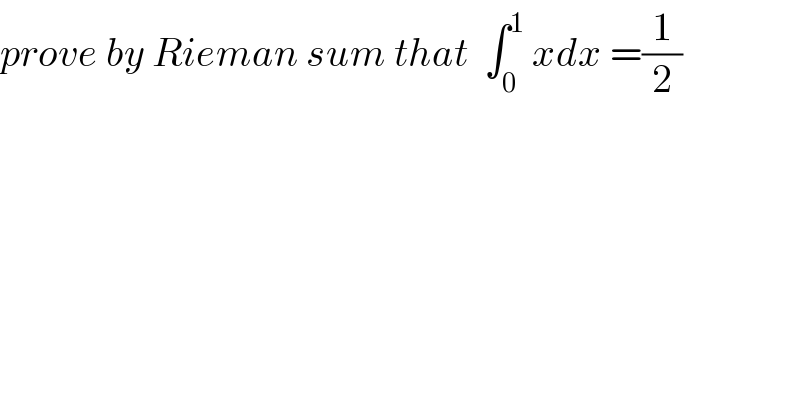
$${prove}\:{by}\:{Rieman}\:{sum}\:{that}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{xdx}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 12/Aug/19
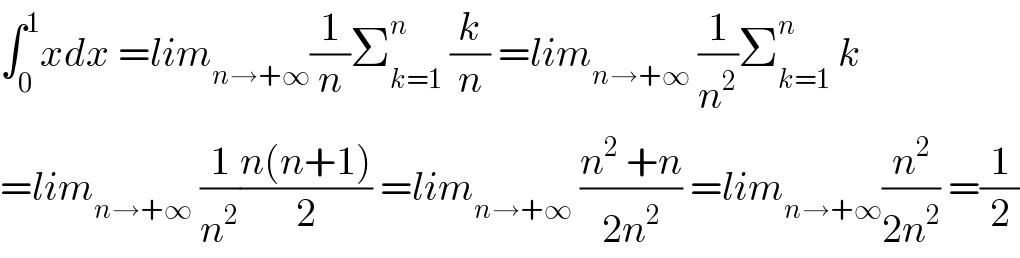
$$\int_{\mathrm{0}} ^{\mathrm{1}} {xdx}\:={lim}_{{n}\rightarrow+\infty} \frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}}{{n}}\:={lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\sum_{{k}=\mathrm{1}} ^{{n}} \:{k} \\ $$$$={lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:={lim}_{{n}\rightarrow+\infty} \:\frac{{n}^{\mathrm{2}} \:+{n}}{\mathrm{2}{n}^{\mathrm{2}} }\:={lim}_{{n}\rightarrow+\infty} \frac{{n}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
